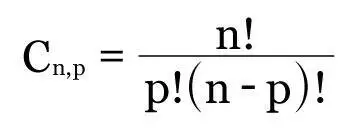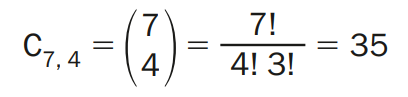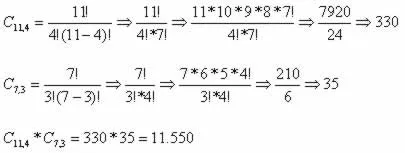A análise combinatória é uma área da matemática que estuda os diferentes arranjos e combinações de elementos de um conjunto. Uma das técnicas mais comuns utilizadas na análise combinatória é a combinação, que consiste em escolher um determinado número de elementos de um conjunto, sem levar em consideração a ordem em que são escolhidos.
As combinações são úteis em muitas áreas da matemática e em outras disciplinas, como na probabilidade, na estatística e nas ciências da computação. Para calcular o número de combinações possíveis de um conjunto, é utilizada a fórmula de combinação, que é dada por:
onde "n" é o número total de elementos do conjunto, "p" é o número de elementos escolhidos e "!" representa o fatorial do número correspondente.
Por exemplo, se tivermos um conjunto de 5 elementos (A, B, C, D, E) e quisermos escolher 3 deles, podemos calcular o número de combinações possíveis da seguinte maneira:
C(5, 3) = 5! / (3! * (5 - 3)!)
C(5, 3) = 120 / (6 * 2)
C(5, 3) = 10
Portanto, há 10 combinações possíveis de escolher 3 elementos de um conjunto de 5 elementos.
As combinações também podem ser representadas por meio de diagramas de árvore ou de tabela, dependendo do contexto do problema. Essas representações visuais podem ajudar a entender melhor as diferentes combinações possíveis e a facilitar os cálculos.
Exemplos 1: Deseja-se formar uma comissão de três membros e dispõe-se de dez funcionários. Quantas comissões podem ser formadas?
Solução: Notemos que cada comissão é um subconjunto de três elementos (pois em cada comissão não importa a ordem dos elementos). Logo, o número de comissões é:
Solução: Cada escolha de 4 lugares corresponde a uma combinação dos 7 elementos, tomados 4 a 4, pois a ordem dos números escolhidos não interessa (escolher os lugares 1, 2, 4, 7 é o mesmo que escolher os lugares 7, 2, 4, 1). Logo, o resultado procurado é:
Solução: Notemos que a ordem em que o aluno escolher as 10 questões não interessa. Por exemplo, resolver as questões 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 é o mesmo que resolver as questões 10, 9, 8, 7, 6, 5, 4, 3, 2, 1.
Logo, cada maneira de escolher 10 questões é uma combinação das 15 questões, tomadas 10 a 10, isto é:
Solução:
Goleiros: C3,1
Zagueiros: C8,4
Meio campistas: C10,4
Atacantes: C6,2
C3,1 * C8,4 * C10,4 * C6,2 = 3 * 70 * 210 * 15 = 661 500 maneiras de o time ser formado
Exemplos 5: Em uma sala de aula existem 12 alunas, onde uma delas chama-se Carla, e 8 alunos, onde um deles atende pelo nome de Luiz. Deseja-se formar comissões de 5 alunas e 4 alunos. Determine o número de comissões, onde simultaneamente participam Carla e Luiz.
Solução:
Comissão de alunas será dada por: C11,4
Comissão de alunos será composta por: C7,3
O número de comissões, respeitando a condição imposta, será de 11 550.
Exemplos 6: Um pesquisador científico precisa escolher três cobaias, num grupo de oito cobaias. Determine o número de maneiras que ele pode realizar a escolha.
Solução:
C8,3
O pesquisador pode realizar a escolha de 56 maneiras.