A Análise Combinatória visa desenvolver métodos que permitam contar o número de elementos de um conjunto, sendo estes elementos agrupamentos formados sob certas condições.
À primeira vista pode parecer desnecessária a existência desses métodos. Isto de fato é verdade, se o número de elementos que queremos contar for pequeno. Entretanto, se o número de elementos a serem contados for grande, esse trabalho torna-se quase impossível sem o uso de métodos especiais.
Vejamos alguns exemplos. Usaremos a notação #M para indicar o número de elementos de um conjunto M.
Exemplos 1: A é o conjunto de números de dois algarismos distintos formados a partir dos dígitos 1, 2 e 3.
A = {12, 13, 21, 23, 31, 32} e #A = 6
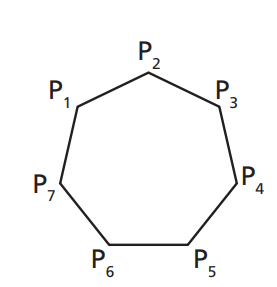
Exemplos 2: B é o conjunto das diagonais de um heptágono.
LISTA DE EXERCÍCIOS PRINCIPIO FUNDAMENTAL DA CONTAGEM
Exemplos 3: C é o conjunto das sequências de letras que se obtêm, mudando a ordem das letras da palavra ARI (anagramas da palavra ARI).C = {ARI, AIR, IRA, IAR, RAI, RIA} e #C = 6
Exemplos 4: D é o conjunto de números de três algarismos, todos distintos, formados a partir dos dígitos 1, 2, 3, 4, 5, 6, 7, 8.
D = {123, 124, 125, ..., 875, 876}
Pode-se perceber que é trabalhoso obter todos os elementos (agrupamentos) desse conjunto e depois contá-los. Corre-se o risco de haver omissão ou repetição de agrupamentos. Usando técnicas que iremos estudar adiante, veremos que #D = 336.
Princípio fundamental da contagem
O princípio fundamental da contagem é uma regra básica da matemática que se aplica quando se deseja calcular o número total de possibilidades de um evento composto por uma série de etapas ou escolhas.
Em termos simples, o princípio fundamental da contagem afirma que, se houver "m" maneiras de realizar uma primeira tarefa e "n" maneiras de realizar uma segunda tarefa, então o número total de maneiras de realizar as duas tarefas em sequência é o produto de "m" e "n".
Em outras palavras, se um evento pode ocorrer em "m" maneiras diferentes e um segundo evento pode ocorrer em "n" maneiras diferentes, então o número total de maneiras que ambos os eventos podem ocorrer em sequência é "m x n".
Esse princípio é frequentemente usado em problemas de probabilidade, combinatória e estatística, onde se precisa calcular o número total de resultados possíveis em situações que envolvem várias etapas ou escolhas.
Exemplos 1: Temos três cidades X, Y e Z. Existem quatro rodovias que ligam X com Y e cinco que ligam Y com Z. Partindo de X e passando por Y, de quantas formas podemos chegar até Z?
Sejam: A o conjunto das rodovias que ligam X com Y e B o conjunto das rodovias que ligam Y com Z:
A = {a1 , a2 , a3 , a4 } e B = {b1 , b2 , b3 , b4 , b5 }
4 X 5 = 20
Exemplos 2: Quantos números com dois algarismos distintos podemos formar com os dígitos 1, 2, 3, 4, 5, 6, 7 e 8?
Então o resultado procurado será 8 ⋅ 7 = 56
Observemos que o diagrama de árvore pode ser usado para obtermos os números formados, notando apenas que, uma vez tomado um elemento na 1ª etapa do diagrama, ele não poderá aparecer na 2ª etapa.
Exemplo 3: Uma pessoa lança uma moeda sucessivamente até que ocorram duas caras consecutivas, ou quatro lançamentos sejam feitos, o que primeiro ocorrer. Quais as sequências de resultados possíveis?