Explorando a Função Seno: Propriedades, Gráficos e Aplicações

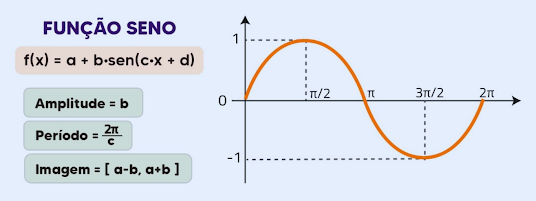
Introdução à função seno:

A função seno é uma das funções trigonométricas fundamentais e descreve a relação entre os lados de um triângulo retângulo. Ela é representada pela função

$�(�)=\sin (�)$,

onde $�$ é o ângulo em radianos. Aqui estão alguns aspectos importantes sobre a função seno:

• Definição básica: A função seno ($\sin (�)$) é definida como a razão entre o lado oposto e a hipotenusa de um triângulo retângulo. Em um triângulo retângulo com um ângulo $�$, o seno desse ângulo é dado pela razão $\frac{\text{oposto}}{\text{hipotenusa}}$.

• Origem e história: O estudo das funções trigonométricas remonta aos antigos matemáticos gregos, como Hiparco de Niceia e Ptolomeu, que os utilizaram para modelar movimentos astronômicos. Desde então, as funções trigonométricas têm desempenhado um papel fundamental em várias áreas da matemática, ciência e engenharia.

• Símbolos: A função seno é comumente representada pelo símbolo $\sin$, e sua forma abreviada é frequentemente usada em expressões matemáticas.

• 

A função seno é uma função periódica, o que significa que ela se repete em intervalos regulares ao longo do eixo dos $�$ (ângulos). O período padrão da função seno é $2�$ radianos, o que significa que a função seno se repete a cada $2�$ radianos.

Propriedades da função seno:

A função seno $\sin (�)$ possui várias propriedades importantes que são fundamentais para entender seu comportamento. Aqui estão algumas das propriedades mais relevantes:

• Período e amplitude: A função seno é uma função periódica, o que significa que ela se repete em intervalos regulares ao longo do eixo dos $�$ (ângulos). O período padrão da função seno é $2�$ radianos. Isso significa que o gráfico da função seno se repete a cada $2�$ radianos. A amplitude da função seno é a metade da distância vertical entre o valor máximo e o valor mínimo da função. A amplitude padrão da função seno é $1$, o que significa que a função seno oscila entre $-1$ e $1$.

• Simetria: A função seno é uma função ímpar, o que significa que é simétrica em relação à origem do plano cartesiano. Matematicamente, isso pode ser expresso como $\sin (-�)=-\sin (�)$. Isso implica que a função seno é simétrica em relação ao eixo vertical (eixo dos $�$).

• Valores máximos e mínimos: Os valores máximos e mínimos da função seno ocorrem nos pontos onde a função atinge $1$ e $-1$, respectivamente. Esses pontos ocorrem em intervalos regulares de $2�$ radianos. Assim, os valores máximos da função seno ocorrem em $\frac{�}{2}+2��$ radianos e os valores mínimos ocorrem em $-\frac{�}{2}+2��$ radianos, onde $�$ é um número inteiro.

• Interpretação geométrica: Geometricamente, o valor do seno de um ângulo $�$ é a coordenada $�$ do ponto na unidade do círculo trigonométrico correspondente a $�$. Isso significa que o valor do seno de um ângulo é igual à coordenada $�$ do ponto onde a linha que forma o ângulo intercepta a circunferência do círculo trigonométrico.

• Gráficos da função seno:

  Os gráficos da função seno ($\sin (�)$) são fundamentais para visualizar seu comportamento periódico e entender suas características. Aqui estão alguns aspectos importantes sobre os gráficos da função seno:

• Plotagem do gráfico: Para plotar o gráfico da função seno, podemos atribuir valores para $�$ (ângulos em radianos) e calcular os valores correspondentes de $\sin (�)$. Ao fazer isso para vários valores de $�$ em um intervalo específico, podemos obter uma série de pontos que representam o comportamento da função seno nesse intervalo. Conectando esses pontos suavemente, obtemos o gráfico da função seno.

• 
  
  

• Ciclos e periodicidade: O gráfico da função seno é caracterizado por ciclos repetitivos. Cada ciclo completo corresponde a um período da função seno, que é $2�$ radianos. Isso significa que o gráfico da função seno se repete a cada $2�$ radianos ao longo do eixo dos $�$. Dentro de um período, a função seno oscila entre seus valores máximos e mínimos.

• Relação entre o ângulo e o valor da função seno: No gráfico da função seno, o eixo horizontal representa os valores do ângulo $�$ em radianos, enquanto o eixo vertical representa os valores da função $\sin (�)$. À medida que o ângulo $�$ aumenta, a função seno oscila entre $-1$ e $1$, conforme ilustrado pelo gráfico sinusoidal.

• Pontos notáveis: Alguns pontos notáveis nos gráficos da função seno incluem os máximos e mínimos da função, que ocorrem nos pontos onde a função atinge $1$ e $-1$, respectivamente. Além disso, os pontos de interceptação do eixo dos $�$ são os zeros da função, onde $\sin (�)=0$.

• Simetria: Como mencionado anteriormente, a função seno é uma função ímpar, o que implica que seu gráfico é simétrico em relação à origem. Isso significa que a parte do gráfico à direita do eixo vertical (positiva) é uma imagem espelhada da parte à esquerda do eixo (negativa).

• Identidades trigonométricas envolvendo a função seno:

  As identidades trigonométricas são relações fundamentais entre as funções trigonométricas, incluindo a função seno. Aqui estão algumas das identidades mais importantes envolvendo a função seno:

  • Identidade fundamental do seno: A identidade fundamental do seno afirma que para qualquer ângulo $�$, temos ${\sin }^2(�)+{\cos }^2(�)=1$. Essa é uma das identidades mais básicas e importantes da trigonometria, conhecida como identidade pitagórica. Ela estabelece a relação entre os valores do seno e do cosseno de um ângulo no contexto de um círculo unitário.

  • Identidade da tangente: Outra identidade útil é derivada da identidade fundamental do seno e diz que $\tan (�)=\frac{\sin (�)}{\cos (�)}$. Esta identidade relaciona a função tangente com as funções seno e cosseno.

  • Identidades de adição e subtração: As identidades de adição e subtração do seno são usadas para decompor ou combinar senos de ângulos diferentes. Por exemplo, a identidade $\sin (�+�)=\sin (�)\cos (�)+\cos (�)\sin (�)$ expressa o seno da soma de dois ângulos em termos dos senos e cossenos dos ângulos individuais.

  • Identidades para ângulos complementares e suplementares: Para ângulos complementares (que somam $90^{\circ }$ ou $\frac{�}{2}$ radianos) e suplementares (que somam $180^{\circ }$ ou $�$ radianos), existem identidades específicas. Por exemplo, para ângulos complementares $�$ e $�$, temos $\sin (�)=\cos (�)$ e $\cos (�)=\sin (�)$.

  • Outras identidades: Existem muitas outras identidades envolvendo a função seno, derivadas de suas propriedades e das relações entre as funções trigonométricas. Estas incluem identidades de duplicação, identidades de metade do ângulo, entre outras.

  Cálculo com a função seno:

  O cálculo com a função seno envolve operações como diferenciação e integração, que são essenciais para analisar o comportamento da função seno e resolver uma variedade de problemas matemáticos e científicos. Aqui estão alguns aspectos importantes do cálculo com a função seno:

  • Derivadas da função seno: A derivada da função seno ($\sin (�)$) em relação ao ângulo $�$ é a função cosseno ($\cos (�)$), ou seja, $\frac{�}{��}[\sin (�)]=\cos (�)$. Isso significa que a taxa de variação instantânea da função seno em relação ao ângulo é dada pela função cosseno.

  • Integrais da função seno: A integral indefinida da função seno ($\sin (�)$) em relação ao ângulo $�$ é a função negativa do cosseno ($-\cos (�)$), acrescida de uma constante de integração. Em outras palavras, $\int \sin (�)��=-\cos (�)+�$, onde $�$ é a constante de integração. A integral definida da função seno também pode ser calculada usando várias técnicas de integração.

  • Aplicações da derivada da função seno: A derivada da função seno é útil em problemas que envolvem taxa de variação, como no estudo de oscilações, movimento harmônico simples e fenômenos ondulatórios. Por exemplo, a derivada da função seno pode ser usada para determinar a velocidade de um objeto em movimento oscilatório em um determinado momento.

  • Aplicações das integrais da função seno: As integrais da função seno são comumente usadas em problemas que envolvem o cálculo de áreas sob curvas senoidais ou o cálculo de deslocamentos em movimentos oscilatórios. Por exemplo, a integral da função seno pode ser usada para determinar o deslocamento total de um objeto em movimento harmônico simples ao longo de um intervalo de tempo específico.

• 
  

•