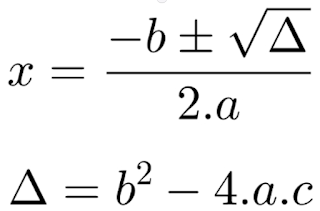A função quadrática é uma das ferramentas mais poderosas e versáteis da matemática, sendo fundamental em diversas áreas, desde a física até a economia. Neste artigo, vamos explorar os elementos essenciais da função quadrática, desvendando seus mistérios e revelando a beleza por trás das parábolas.
Definição: A Base da Função Quadrática
A função quadrática é uma expressão matemática de segundo grau, geralmente representada por f(x) = ax² + bx + c, onde a, b, e c são coeficientes constantes e a ≠ 0.
Essa função é conhecida por gerar uma curva em forma de parábola quando plotada em um sistema de coordenadas cartesianas.
Exercícios Função Quadrática: Enem e Concursos
Zero ou Raiz e Fórmula de Bhaskara: A Busca pelas Soluções
A busca pelas raízes da função quadrática, os pontos onde f(x) atinge o valor zero, nos leva à fórmula de Bhaskara. Essa fórmula mágica,
nos revela os valores de x que tornam a função igual a zero. O discriminante Delta (∆ = b² - 4ac) dentro da raiz quadrada desempenha um papel crucial na determinação do número e natureza das raízes.
Saiba mais sobre as Funções do Segundo Grau
Vértice da Parábola: O Ponto de Destaque
Ao analisarmos uma parábola, deparamo-nos com seu ponto de destaque, o vértice. Esse ponto, dado por (-b/2a, f(-b/2a)) ou (-b/2a, -∆/4a) , fornece informações sobre o ponto de mínimo ou máximo da função quadrática, dependendo do sinal de a. É aqui que a parábola atinge seu ponto mais baixo ou mais alto.
Discriminante: Decifrando as Possibilidades
O discriminante, (∆ = b² - 4ac), não é apenas um número; é uma janela para as possibilidades.
Se ∆ > 0, temos duas raízes reais distintas.
Se ∆ = 0, temos duas raízes reais iguais.
Se ∆ < 0, não temos raízes reais.
Gráfico: A Visualização da Função Quadrática
Nada como um gráfico para dar vida a uma função matemática. O gráfico da função quadrática é uma elegante parábola, revelando sua concavidade e amplitude. A direção da abertura da parábola é ditada pelo sinal de a e do ∆, tornando-se uma peça fundamental na interpretação visual da função. Saiba mais...
Interpretação Geométrica: Compreendendo as Coeficientes
Cada coeficiente da função quadrática tem um papel geométrico importante. a determina a largura e a orientação da parábola, b influencia a posição horizontal do vértice, e c determina a posição vertical do vértice. Compreender esses elementos permite-nos visualizar como a função se comporta.
Máximo e Mínimo: O Poder do Coeficiente a
O coeficiente a é a chave para determinar se a parábola tem um ponto mínimo ou máximo. Quando a > 0, a função tem um mínimo, e quando a < 0, a função possui um máximo. Essa propriedade é crucial na modelagem de situações do mundo real.
Inequação Quadrática: Expandindo as Possibilidades
Além de resolver equações, a função quadrática também nos guia na resolução de inequações quadráticas. Ao integrar operadores de desigualdade à função, exploramos intervalos nos quais a função é positiva ou negativa, ampliando seu alcance e utilidade.
Conclusão: Desbravando Novos Horizontes com a Função Quadrática
A função quadrática, com sua elegância matemática e aplicabilidade prática, desempenha um papel fundamental na compreensão do mundo ao nosso redor. Ao dominarmos os conceitos de zero, vértice, discriminante e inequação, abrimos portas para a solução de problemas complexos e a modelagem de fenômenos diversos. A função quadrática é verdadeiramente uma peça chave no quebra-cabeça da matemática, desafiando-nos a explorar seu universo infinito de possibilidades.