Analise Combinatória ⇒ FGV-SP Matemática 2024 - Unificado - 1ª fase

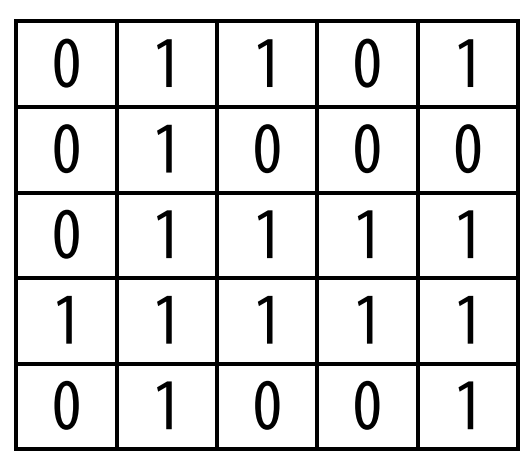
(FGV - SP 2024) Uma tabela 5 x 5 é totalmente preenchida apenas com 0’s e 1’s, de tal maneira que uma de suas linhas tem a soma dos elementos igual a 1, outra tem soma igual a 2, outra tem soma igual a 3, outra tem soma igual a 4 e a restante tem soma igual a 5. O mesmo ocorre com as colunas dessa tabela, tendo somas iguais a 1, 2, 3, 4 e 5. A figura mostra um exemplo:

O número de tabelas diferentes que satisfazem as condições do enunciado é: 

A) 25 

B) 1225 

C) 625

 D) 120 

E) 14400 

👉 Solução em vídeo

Solução

Resolução 1) Cada uma das 5 linhas da tabela pode permutar num total de 5! = 120 possibilidades.

2) Da mesma forma, existem 5! = 120 possibilidades de se permutar as 5 colunas da tabela.

3) Portanto, existem 120 . 120 = 14 400 tabelas possíveis.

Resposta: E