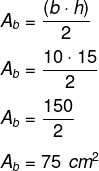Volume de Sólidos Geométricos

 Volume de Sólidos Geométricos

O volume é uma grandeza que descreve o espaço ocupado por um objeto tridimensional. Quando lidamos com sólidos geométricos, o cálculo do volume desempenha um papel fundamental em diversas aplicações, desde a construção civil até a matemática pura. Neste artigo, exploraremos como calcular o volume de alguns sólidos geométricos comuns.

1. Cubo

Um cubo é um sólido com seis faces quadradas congruentes. Para calcular o volume de um cubo, você pode usar a fórmula:

$�={�}^3$

Onde "V" é o volume e "L" é o comprimento de um lado do cubo.

2. Paralelepípedo

Um paralelepípedo é um sólido com seis faces retangulares. O volume de um paralelepípedo é calculado multiplicando-se o comprimento (L), a largura (W) e a altura (H):

$�=�\cdot �\cdot �$

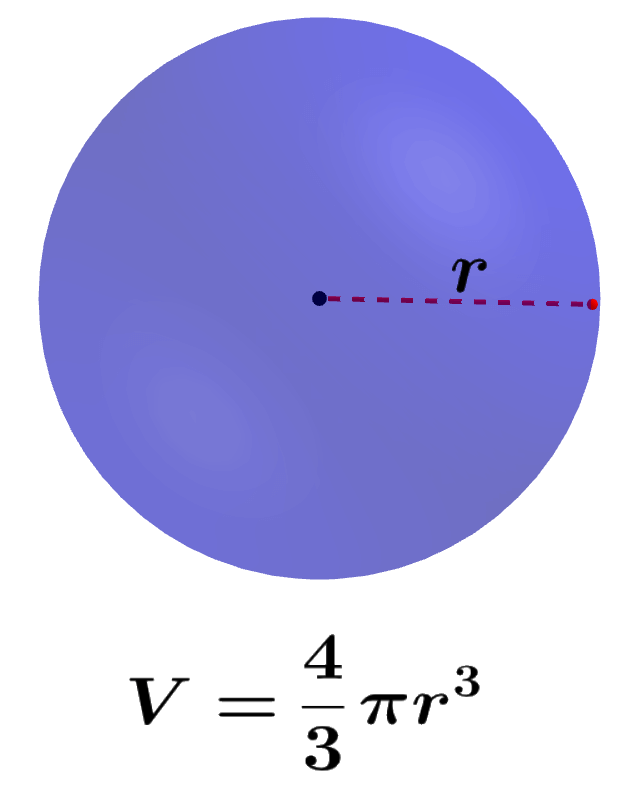
3. Esfera

Uma esfera é um sólido simétrico, e seu volume é dado pela fórmula:

$�=\frac{4}{3}�{�}^3$

Onde "V" é o volume e "r" é o raio da esfera.

4. Cilindro

Um cilindro possui duas bases circulares e uma superfície lateral que é retangular quando desenrolada. O volume de um cilindro é calculado usando a seguinte fórmula:

$�=�{�}^2ℎ$

Onde "V" é o volume, "r" é o raio da base, e "h" é a altura.

Leia também

Teorema de Pitágoras

Ângulos e Retas

O papel da matemática na revolução científica:

5. Cone

O cone tem uma base circular e uma superfície lateral que converge para um ponto chamado ápice. Seu volume é calculado usando a fórmula:

$�=\frac{1}{3}�{�}^2ℎ$

Onde "V" é o volume, "r" é o raio da base e "h" é a altura.

6. Pirâmide

Uma pirâmide é um sólido com uma base poligonal e faces triangulares que convergem para um ponto no topo. O volume de uma pirâmide é calculado usando a fórmula:

$�=\frac{1}{3}{�}_{�}ℎ$

Onde "V" é o volume, "A_b" é a área da base e "h" é a altura.

7. Prismas

Um prisma é um sólido com duas bases congruentes e faces laterais retangulares. O volume de um prisma é dado pela fórmula:

$�={�}_{�}\cdot ℎ$

Onde "V" é o volume, "A_b" é a área da base e "h" é a altura.

Em resumo, o cálculo do volume de sólidos geométricos é essencial para resolver uma variedade de problemas em matemática, física, engenharia e muitas outras disciplinas. Conhecer as fórmulas corretas para calcular o volume de diferentes sólidos é fundamental, pois permite a determinação precisa do espaço ocupado por esses objetos tridimensionais. A compreensão desses conceitos é crucial para diversas aplicações práticas e teóricas em diversas áreas do conhecimento.

Exercícios resolvidos sobre volume dos sólidos geométricos

Questão 1 - (Fei) De uma viga de madeira de seção quadrada de lado L =10 cm, extrai-se uma cunha de altura h = 15 cm, conforme a figura. O volume da cunha é:

A) 250 cm³

B) 500 cm³

C) 750 cm³

D) 1000 cm³

E) 1250 cm³

V = Ab · h

V = 75 · 10

V = 750 cm

Leia também

Teorema de Pitágoras

Ângulos e Retas

O papel da matemática na revolução científica: