A figura abaixo mostra o esquema de uma represa. A ponte, representada pelo segmento
AB, pode ser medida com auxílio de uma trena.
m(AB) = 164 m
Já o ângulo BAB pode ser medido diretamente com o auxílio de um teodolito (instrumento
de precisão para medir ângulos horizontais e verticais): m(BAC) = 75°.
Existem, contudo, muitas situações em que não é possível medir diretamente um ângulo ou a
distância entre dois pontos, como por exemplo na figura acima, quando se deseja obter a distância
entre os pontos A, localizado em um extremo da ponte, e C, localizado na margem oposta da represa.
Procurando resolver problemas dessa natureza, os matemáticos estabeleceram importantes relações entre as medidas dos ângulos e as medidas dos lados de um triângulo. A área
da Matemática que estuda essas relações é chamada de Trigonometria.
A palavra "trigonometria", de origem grega, significa “medida de triângulos”. Embora não
tenhamos informações precisas sobre a origem dos estudos trigonométricos, há registros de
sua aplicação por babilônios e antigos egípcios, especialmente na Agrimensura e na Astronomia.
Sabe-se que a Trigonometria era usada, por exemplo, para determinar distâncias que
não podiam ser medidas com instrumentos, como a distância entre os planetas. Para tais
cálculos, eram aplicadas relações entre as medidas dos lados e as medidas dos ângulos
de um triângulo.
As razões trigonométricas seno, cosseno e tangente
Seno de um ângulo agudo
Considere a figura ao lado.
Os triângulos retângulos OAB, OCD e OEF são
semelhantes pelo caso AA, pois têm em comum
o ângulo de medida a (também chamado de
ângulo a) e um ângulo reto.
Como os triângulos OAB e OCD são semelhantes e os lados correspondentes são proporcionais, podemos escrever:
Os triângulos OAB e OEF são semelhantes, portanto os lados correspondentes são proporcionais:
Observe as duas proporções que destacamos acima: Da propriedade fundamental das proporções, podemos escrever: Há infinitos outros triângulos retângulos que têm como ângulo interno o ângulo a e que,
por isso, também são semelhantes aos triângulos OAB, OCD e OEF.
Para todos esses triângulos retângulos, a razão entre a medida do cateto oposto ao ângulo α e a medida da hipotenusa é constante. A essa razão constante chamamos seno do ângulo α e
a indicamos por sen α.
Seno de um ângulo agudo de um triângulo retângulo é a razão entre a medida
do cateto oposto a esse ângulo e a medida da hipotenusa.
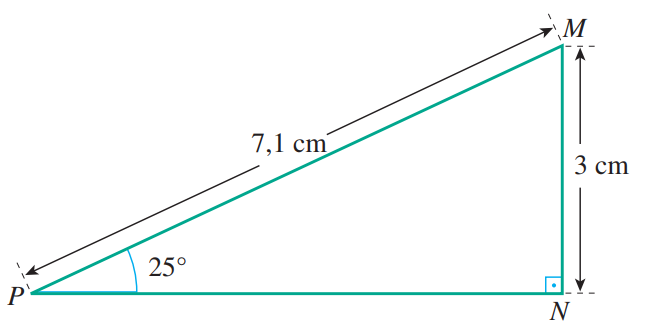
Considerando qualquer um desses triângulos, temos:Acompanhe um exemplo.No triângulo MNP, vamos calcular o seno do ângulo interno P, que mede 25°.
Cosseno e tangente de um ângulo agudo
Considere novamente os triângulos retângulos OAB, OCD e OEF.
Como já vimos, os triângulos OAB, OCD e OEF são semelhantes.
De modo análogo ao que fizemos para a razão seno, dessa
semelhança obtemos:

A essa razão constante chamamos de cosseno do ângulo α e a indicamos por cos α.
Cosseno de um ângulo agudo de um triângulo retângulo é a razão entre a medida
do cateto adjacente a esse ângulo e a medida da hipotenusa.
Para qualquer um desses triângulos, temos:
A essa razão constante chamamos de tangente do ângulo α e a indicamos por tg α.
Tangente de um ângulo agudo de um triângulo retângulo é a razão entre a medida
do cateto oposto e a medida do cateto adjacente a esse ângulo.
Considerando qualquer dos triângulos da figura anterior, temos:
Exemplo
Qual o comprimento da sombra de uma árvore de 5m de altura quando o sol está a 30° acima do horizonte?
Tg B = AC / AB = 5/s
Uma vez que B = 30° temos que a:
Tg B = 30° = √3/3 = 0,577
Logo,
0,577 = 5/s
s = 5/0,577
s = 8,67
Portanto, o tamanho da sombra é de 8,67 metros.
Questão que caiu no Enem 2023