01 - A parte interior de uma taça foi gerada pela rotação de uma parábola em torno de um eixo z, conforme mostra a figura.
A função real que expressa a parábola, no plano cartesiano da figura, é dada pela lei f(x) = 3/2 x² – 6x + C, onde C é a medida da altura do líquido contido na taça, em centímetros. Sabe-se que o ponto V, na figura, representa o vértice da parábola, localizado sobre o eixo x.
Nessas condições, a altura do líquido contido na taça, em centímetros, é
A 1.
B 2.
C 4.
D 5.
E 6.
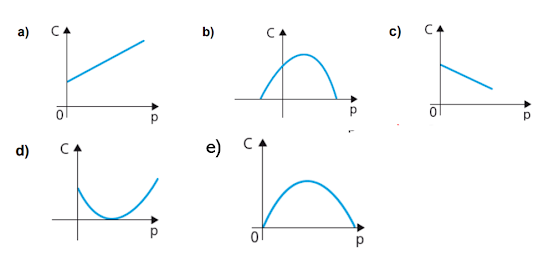
2 - Admita que determinado lago possa suportar uma população máxima de 10.000 peixes e que, para uma pequena população inicial p, a rapidez de seu crescimento C seja dada pela função C (p) = k . p . (10000 – p), sendo k uma constante positiva e 0 <p ≤10000.
O gráfico cartesiano que melhor representa a função C(p), para p real, é
3 - (UNIME 2016 – Modificada) Foram feitas três medições da temperatura de um paciente, a intervalos de 1h, cujos resultados, em ordem, foram 37 ºC, 40,5 ºC e 39 ºC.
Nesse período, a temperatura variou como uma função do 2º grau, e consideramos para a primeira medição t = 0.
Qual a função que relaciona a temperatura T, em ºC, desse paciente t horas após a primeira medição?
a) T(t) = -1,5t² + 8t + 37
b) T(t) = -0,5t² + 12t + 39
c) T(t) = -2,5t² + 6t + 37
d) T(t) = -1,5t² + 4t + 39
e) T(t) = -0,5t² + 2t + 40,54 - (CMRJ 2018) Uma ponte metálica, em forma de arco de parábola, será construída. Sua sustentação será feita com seis pendurais metálicos, três de cada lado, distando 30 m um do outro, como ilustra a figura abaixo.
Sabendo que a ponte tem 40 m de altura, quantos metros de pendurais serão necessários para a construção desta ponte?
a) 120 m.
b) 140 m.
c) 160 m.
d) 180 m.
e) 200 m.
5 - Uma pessoa começa a receber um medicamento através de um soro e a quantidade Q, em mg, do mesmo em sua corrente sanguínea varia de acordo com a função Q(t) –t² + 6t + 20, sendo t o tempo em horas desde o início da aplicação do soro.
a) Após quanto tempo do início da aplicação do soro, a quantidade do medicamento na corrente sanguínea é máxima?
b) Qual é essa quantidade máxima de medicamento?