Exercício Função Quadrática ou do Segundo Grau Resolvido
Admita que determinado lago possa suportar uma população máxima de 10.000 peixes e que, para uma pequena população inicial p, a rapidez de seu crescimento C seja dada pela função
C(p) = k . p . (10000 – p), sendo k uma constante positiva e 0 <p ≤10000.
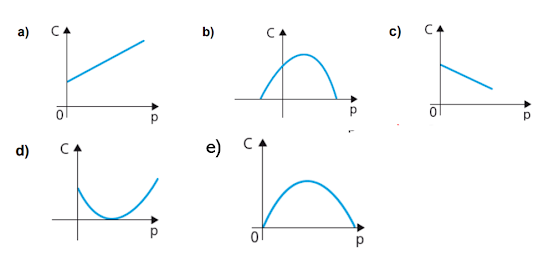
O gráfico cartesiano que melhor representa a função C(p), para p real, é
Solução
Aplicando a distributiva em C (p) = k . p . (10000 – p), temos que C (p) = 10000. p – k .p²
Essa é uma função do segundo grau (gráfico parábola) com a = -k, pois k é positivo (concavidade para baixo) e c = 0 (passa pela origem).
Desse modo, alternativa e



Tenho muita dificuldade em função quadratica, sofri e sofro com isso gostaria de ver exercícios resolvido. Obrigado
ResponderExcluir