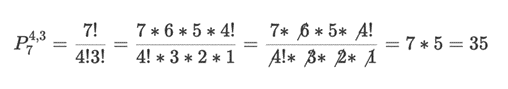ENEM 2020 Regular
Três amigos, André, Bernardo e Carlos, moram em um condomínio fechado de uma cidade. O quadriculado representa a localização das ruas paralelas e perpendiculares, delimitando quadras de mesmo tamanho nesse condomínio, em que nos pontos A, B e C estão localizadas as casas de André, Bernardo e Carlos, respectivamente.
a) 4.
b) 14.
c) 17.
d) 35.
e) 48.
Solução passo a passo
Este exercício quer saber quantas formas
diferentes André tem para chegar na casa de Bernardo, sem passar pela casa de
Carlos.
Logo, para fazermos uma análise como esta
a forma mais fácil é você contabilizar todas as formas possíveis (incluindo
aquelas que passam por Carlos) e depois descontar as possibilidades que passam
pela casa de Carlos.
Portanto, no primeiro momento vamos
calcular as possibilidades totais. Este é um exercício claro de permutação com
repetição. Para os casos totais vamos ter 4 deslocamentos para a direita e 3
deslocamentos pra cima, sendo assim em nossa permutação:
Portanto, temos 35 possibilidades no
total. Agora, vamos ter que calcular quantas são as possibilidades que passam
pelo Carlos. Para isso, primeiro calculamos os caminhos de A até C, depois
calculamos os caminhos de C até B, pois com essas duas contas vamos saber os
caminhos totais que passam por C, uma vez que os caminhos até C não representam
as possibilidades até B, que é o solicitado pelo exercício.
Para A até C, temos 2 deslocamentos a
direita e 2 para cima, logo:
Agora, para C até B, temos 2
deslocamentos pra a direita e 1 para cima, logo:
Agora, para sabermos as possibilidades
totais multiplicamos um pelo outro:
Por fim, descontamos os casos que passam
por C dos casos totais, logo:
35 - 18 = 17
Sendo assim, a alternativa correta é C.