Triângulos: definição, classificação e propriedades

 Triângulos em construções

Observe a foto ao lado, que mostra a cobertura das casas. Veja que o telhado será apoiado em estruturas triangulares, e isso ocorre porque os engenheiros civis sabem que os triângulos possuem características muito especiais. É por esse motivo que vamos estudá-los.

Na figura ao lado há três segmentos consecutivos e não colineares, AB, BC e CA. Juntos, esses segmentos formam um polígono (ou linha poligonal fechada) chamado triângulo. Indicamos o triângulo ABC por ∆ABC. 

Em um triângulo ABC, os pontos A, B e C são chamados vértices, e os segmentos AB (de medida c), BC (de medida a) e CA (de medida b) são chamados lados.

Os ângulos BAC (ou A ), ABC (ou B ) e ACB (ou C) são chamados ângulos internos do triângulo. Para simplificar a linguagem, é usual dizer: 

• o lado a é o oposto ao ângulo A; 
• o lado b é o oposto ao ângulo B;
• o lado c é o oposto ao ângulo C.

O perímetro de um triângulo,  é a soma das medidas dos seus lados. No triângulo ABC, temos:

  Perímetro: a + b + c

 Classificação de triângulos quanto aos lados

Quando comparamos os lados de um triângulo, três casos podem ocorrer:

1° caso – Os três lados são congruentes. Nesse caso, o triângulo é chamado de equilátero.

2° caso – Dois lados são congruentes. O outro lado é chamado de base do triângulo. Nesse caso, o triângulo é dito isósceles.

3°  caso – Dois lados quaisquer não são congruentes. Nesse caso, o triângulo é dito escaleno. 

Exemplos

1 - O triângulo ao lado não tem dois lados de mesma medida; é, portanto, escaleno. 

O perímetro desse triângulo é: 

35 mm + 28 mm + 20 mm = 83 mm

2 - O triângulo ao lado tem dois lados congruentes; é, portanto, isósceles. 

O perímetro desse triângulo é: 

2 x4 cm + 3 cm = 11 cm

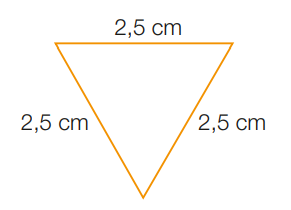
3 - O triângulo ao lado tem os três lados congruentes; é, portanto, equilátero. 

O perímetro desse triângulo é: 

3 x 2,5 cm = 7,5 cm

 

Desigualdade triangular

Se tentássemos construir um triângulo de lados medindo a = 6 cm, b = 3 cm e c = 2 cm, obteríamos a figura ao lado. 

Os arcos não se cruzam. Isso significa que não existe triângulo de lados medindo 6 cm, 3 cm e 2 cm. 

Por que isso acontece? Esse fato é justificado pela propriedade a seguir

Então, dado o triângulo ABC, em que a é medida do lado BC, b é medida do lado AC e c é medida do lado AB, podemos escrever as seguintes relações:

Portanto, podemos saber se existe ou não um triângulo de determinadas medidas comparando a maior delas com a soma das outras duas. O triângulo só existirá se a medida do lado maior for menor que a soma das medidas dos outros dois.

Exemplo 

Vamos verificar se existe um triângulo de lados medindo 9,2 cm, 13,1 cm e 4,7 cm. 

Como a maior medida é 13,1 cm, vamos verificar a soma das outras duas medidas: 

9,2 cm + 4,7 cm = 13,9 cm. 

Como 13,1 < 13,9, existe um triângulo com essas medidas dos lados. Seguindo os passos do tópico “Construindo um triângulo”, construa esse triângulo. 

 

Propriedade da soma dos ângulos internos de um triângulo

Vamos considerar um triângulo ABC e seus ângulos, A, B e C.

Pelo vértice A, vamos traçar uma reta r paralela ao lado BC e marcar os ângulos 1 e 2, como abaixo:

Do paralelismo de r e BC, considerando a transversal AB, decorre que: 

1 ≡ B

Do paralelismo de r e BC, considerando a transversal AC, decorre que: 

2 ≡ C

Substituindo 1 por B e 2 por C na figura, temos:

Adicionando as medidas dos ângulos que têm vértice em A, concluímos que:

Esse resultado é resumido pela propriedade:

 

Classificação dos triângulos quanto aos ângulos

Os triângulos podem ser classificados em relação às medidas dos ângulos internos. Considerando que a soma das medidas dos ângulos de um triângulo é 180°, podem ocorrer as seguintes situações:

• Os três ângulos são agudos. Nesse caso, o triângulo é dito acutângulo.

Por exemplo, o triângulo representado ao lado tem ângulos internos de medidas 50°, 60° e 70°. Note que: 50° + 60° + 70° = 180° 

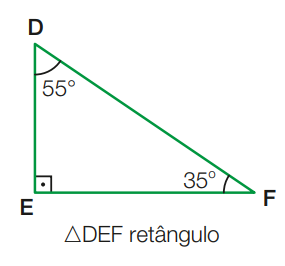
• Um dos ângulos é reto e os outros dois são agudos. Nesse caso, o triângulo é dito retângulo.

Por exemplo, o triângulo representado ao lado tem ângulos internos de medidas 90°, 35° e 55°. Note que: 90° + 35° + 55° = 180° 

• Um dos ângulos é obtuso e os outros dois são agudos. Nesse caso, o triângulo é dito obtusângulo

 Por exemplo, o triângulo representado ao lado tem ângulos internos de medidas 120°, 20° e 40°. Note que: 120° + 20° + 40° = 180°

Propriedade do ângulo externo de um triângulo

Considere o triângulo ABC representado abaixo:

Vamos prolongar o lado BC do triângulo ABC na extremidade C e tomar um ponto X no prolongamento, de modo que a semirreta CX seja oposta à semirreta CB.

Dizemos que o ângulo ACX é um ângulo externo do triângulo ABC. 

Observe que o ângulo externo ê ≡ ACX é adjacente ao ângulo C do triângulo. Mas os ângulos A e B não são adjacentes ao ângulo externo ê.

Observe, ainda, que:

Exemplo 

Qual é o valor de x e y?