Quando falamos de números naturais, sabemos que entre dois deles existe uma quantidade finita de números naturais e que entre dois números naturais consecutivos não existe nenhum número natural. Por exemplo, entre os números 3 e 10 existem exatamente 6 números naturais: 4, 5, 6, 7, 8 e 9.
O mesmo acontece com os números inteiros. Já com os números racionais, a situação é diferente.
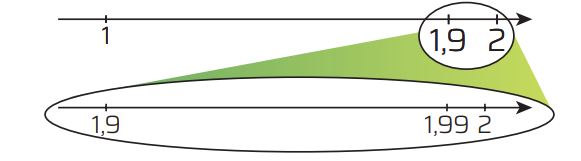
Acompanhe a seguir o que acontece quando tentamos encontrar números racionais entre 1 e 2.
- Considere o intervalo entre os números 1 e 2 na reta numerada.
- Entre esses números existem diversos números, como o número 1,9.
- Já entre 1,9 e 2 existem diversos outros números, como o número 1,99.
- Entre 1,99 e 2 existem ainda vários outros números, como o número 1,999.
Poderíamos continuar esse processo indefinidamente, pois sempre encontraríamos outro número no intervalo. O mesmo aconteceria se escolhêssemos dois outros racionais diferentes.
De fato, o conjunto dos números racionais tem a propriedade de que entre dois números racionais diferentes existe uma infinidade de números racionais.