Triângulo e Semicircunferência: Exercício de Geometria Plana
Sabendo que EP é o raio da semicircunferência de centro em E, como mostra a figura, determine o valor da área mais escura e assinale a opção correta. Dado: número π=3
a) 10 cm2
b) 12 cm2
c) 18 cm2
d) 10 cm2
e) 24 cm2
Solução
Alternativa correta: b) 12 cm2.
A área mais escura é encontrada somando-se a área da semicircunferência com a área do triângulo ABD. Vamos começar calculando a área do triângulo, para isso, note que o triângulo é retângulo.
Vamos chamar o lado AD de x e calcular a sua medida através do teorema de Pitágoras, conforme indicado abaixo:
52= x2 + 32
x2 = 25 - 9
x = √16
x = 4
Conhecendo a medida do lado AD, podemos calcular a área do triângulo:
Precisamos ainda, calcular a área da semicircunferência. Note que o seu raio será igual a metade da medida do lado AD, assim, r = 2 cm. A área da semicircunferência será igual a: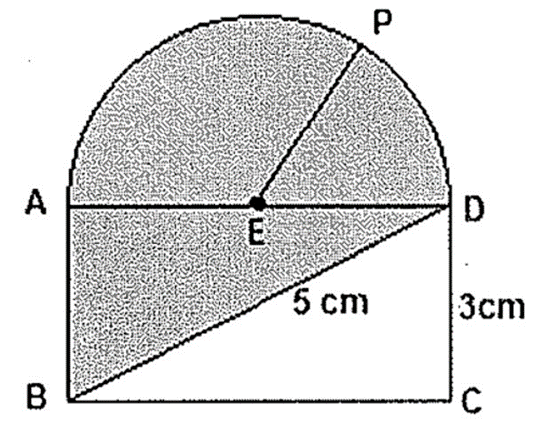


Comentários
Postar um comentário