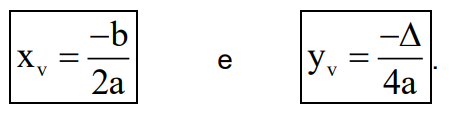Equação de 2º Grau ou Quadrática
Toda equação de 2º grau possui a forma ax2 + bx + c = 0, em a, b e c são
os coeficientes da equação devendo ser números reais e a ¹ 0.
Uma equação em que os três coeficientes sejam diferentes de
zero é chamada de equação completa e são resolvidas através de uma expressão
que ficou conhecida como Fórmula de Bhaskara, em que as raízes (x’ e x’’) são
calculadas em função dos coeficientes da equação.
Inicialmente devemos calcular o discriminante da equação,
mais conhecido como delta (Δ)
D = b² - 4ac
Em seguida, o valor de Δ será usado para calcular as raízes
através da expressão
Por fim, as raízes obtidas serão
Exercício
1 - Resolva as equações:
a) x2 + 9x + 14 = 0
b) x2 − 4x + 4 = 0
c) x2 – 6x + 13 = 0
O valor do discriminante (delta) determina características das raízes da equação, caso existam:
△ > 0: Duas raízes (zeros) reais distintas.
△ = 0: Duas raízes (zeros) reais iguais (raiz dupla).
△ < 0: Não possui raízes (zeros) reais.
➢ As equações a seguir são incompletas e podem ser resolvidas maneiras mais rápidas.
Equação do Segundo Grau Incompleta
Exemplos:
x² + 2x + 1 = 0 → equação do 2º grau completa;
x² – 5x = 0 → equação do 2º grau incompleta;
x² – 25 = 0 → equação do 2º grau incompleta;
3x² = 0 → equação do 2º grau incompleta
Exercício
1 - Encontre as soluções da equação 2x² + 5x = 0.
1º passo: colocar x em evidência.
Reescrevendo a equação colocando x em evidência, temos que:
2x² + 5x = 0
x · (2x + 5) = 0
2º passo: separar a equação produto em dois casos.
Para que a multiplicação entre dois números seja igual a zero, um deles tem que ser igual a zero, no caso, temos que:
x · (2x + 5) = 0
x = 0 ou 2x + 5 = 0
3º passo: encontrar as soluções.
Já encontramos a primeira solução, x = 0, agora falta encontrar o valor de x que faz com que 2x + 5 seja igual a zero, então, temos que:
Então encontramos as duas soluções da equação, x = 0 ou x = -5/2.
2 - Encontre as soluções da equação 3x² – 12 = 0.
Para encontrar as soluções, vamos isolar a variável.
3x² – 12 = 0
3x² = 12
x² = 12 : 3
x² = 4
Ao extrair a raiz no segundo membro, é importante lembrar que existem sempre dois números e que, ao elevarmos ao quadrado, encontramos como solução o número 4 e, por isso, colocamos o símbolo de ±.
x = ±√4
x = ±2
Então as soluções possíveis são x = 2 e x = -2.
Equação do Segundo Grau Completa
As funções que possuem os três coeficientes diferentes de zero são chamadas de funções completas. Caso b = 0 ou c = 0 , as funções são chamadas de funções incompletas.
Gráfico de uma Função Quadrática
O gráfico de toda função de 2° grau é uma parábola. Sua concavidade depende do coeficiente a
Essa parábola poderá ficar disposta basicamente de seis maneiras diferentes (divididas em três situações) a depender da concavidade e da quantidade de vezes que a mesma corta o eixo x.
Quando △ > 0 , o gráfico toca o eixo x em dois pontos.
Quando △ = 0 , o gráfico toca o eixo x em dois pontos.
Quando △ < 0 , o gráfico toca o eixo x em dois pontos.
O(s) ponto(s) em que o gráfico toca o eixo x, caso existam, são as raízes da função. Ou seja, são os valores que tornam a função igual a zero e, consequentemente são a solução da equação ax2 + bx + c = 0.
O ponto de intersecção com o eixo y será o termo independente da função (c) e o(s) ponto(s) de interseção com o eixo x, caso existam, serão as raízes da função (x’ e x’’)
Quando c = 0, o gráfico da função passa pela origem e quando b = 0, o gráfico tem uma simetria em relação ao eixo y.
Para determinar a expressão de uma função f (x) de 2º grau devemos conhecer no mínimo três de seus valores numéricos. A partir desses valores criamos um sistema com os três coeficientes da função (a, b e c) que, ao resolvê-lo, teremos determinado a expressão da função.
➢ Caso um dos valores conhecidos seja f(0), o sistema formado será resolvido de maneira bem mais fácil.
Caso se conheça as duas raízes da função (x’ e x’’), uma maneira mais prática para representar a função de 2º grau é
A vantagem de se representar dessa forma é o fato de termos de descobrir apenas o valor do coeficiente a, entretanto só pode ser usada caso as raízes x’ e x’’ sejam conhecidas.
Estudo do vértice da parábola
Toda parábola ax2 + bx + c = 0 possui um ponto, chamado de vértice que é o ponto em que a função assume seu valor máximo (caso a parábola possua a concavidade voltada para baixo) ou seu valor mínimo (caso a concavidade seja voltada para cima).As coordenadas do vértice V da parábola são:
Distinguimos dois casos.Confira os Exercícios Sobre Função Quadrática ou do Segundo Grau