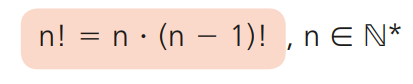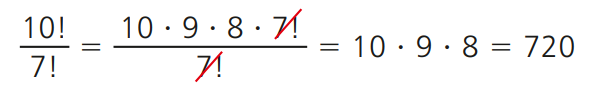Fatorial de um número natural

O fatorial de um número natural é o produto de todos os números naturais de 1 até esse número. É representado pelo símbolo "!" e é calculado da seguinte forma:

N! = N x (N - 1) x (N - 2) x ... x 2 x 1

Por exemplo, o fatorial de 5 é calculado da seguinte maneira:

5! = 5 x 4 x 3 x 2 x 1 = 120

O fatorial de 0 é 1 por convenção:

0! = 1

O fatorial é frequentemente utilizado em matemática para calcular combinações, permutações e resolver problemas de contagem. É um conceito fundamental em teoria de números e probabilidade.

Podemos também prensar como uma função, sendo que a função fatorial de um número natural n é uma operação que envolve o produto de todos os números naturais de 1 a n. Isso é expresso como 

F(n) = n! = 1 x 2 x 3 x 4 ... x n, 

e vale destacar que F(0) = 1. 

Embora não seja uma função comum em linguagens de programação, sua aplicação é amplamente significativa nas ciências.

Dado um número natural n, definimos o fatorial de n (indicado por n!) por meio das relações:

Notemos que, em 3 , o fatorial de n representa o produto dos n primeiros números naturais positivos. Um pouco mais à frente, você vai compreender a “conveniência” de se definir 0! = 1 e 1! = 1. 

Assim, temos, por exemplo: 

2! = 2 x 1 = 2 

3! = 3 x 2 x 1 = 6 

4! = 4 x 3 x 2 x 1 = 24 

5! = 5 x 4 x 3 x 2 x 1 = 120

À medida que n aumenta, o cálculo de n! torna-se mais trabalhoso. Para ajudar, podemos utilizar a seguinte propriedade:

Veja estas simplificações:

Exemplo 1: Para calcularmos o valor de 10!/7!  podemos desenvolver o fatorial do número maior, 10, até chegarmos ao fatorial do menor, 7. 

Temos:

Exemplo 2:  Resolva a equação 

Solução: Como n + 1 > n - 1, desenvolvemos o fatorial de n +1 até chegarmos ao fatorial de n -1:

Lembrando que só se define o fatorial de um número natural, concluímos que o único valor possível é n = 2; então S = {2}. 

EXERCÍCIOS

 

Solução