Intervalos reais: O que são e como representar
O conjunto dos números reais possui também subconjuntos denominados intervalos, nos quais os elementos são determinados por meio de desigualdades. Sejam os números reais a e b, com a < b.
Explicação em vídeo aula
Lista de Exercícios sobre Intervalos Reais
Note as “bolinhas vazias”; elas excluem os valores 3 e 5.
Intervalo aberto à direita e fechado à esquerda de extremos a e b é o conjunto
Existem ainda os seguintes intervalos:
Na resolução de inequações e de outros problemas em que são necessárias operações como união, interseção etc. entre intervalos, podemos utilizar uma representação gráfica.
podemos representá-los como se vê abaixo.
Intervalo aberto de extremos a e b é o conjunto
Exemplo
Note as “bolinhas vazias”; elas excluem os valores 3 e 5.
Intervalo fechado de extremos a e b é o conjunto
Exemplo
Exemplo
Existem ainda os seguintes intervalos:
Observe que o intervalo determina uma semirreta (à esquerda) com origem em 3.
Na resolução de inequações e de outros problemas em que são necessárias operações como união, interseção etc. entre intervalos, podemos utilizar uma representação gráfica.
Exemplo
Dados os intervalos:
podemos representá-los como se vê abaixo.
Determine:
.png)







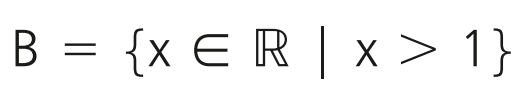








Comentários
Postar um comentário