Encceja é um exame nacional para certificação de competências de jovens e adultos no ensino fundamental. A prova de matemática é uma das disciplinas avaliadas e os gabaritos são fornecidos após a realização do exame. O objetivo é verificar o conhecimento e habilidades dos participantes e fornecer uma certificação para aqueles que atingirem os padrões estabelecidos.
Se você está buscando uma maneira de obter sua certificação de ensino fundamental, o Encceja é a solução perfeita. Uma das disciplinas avaliadas é a matemática, e é importante se preparar adequadamente para essa prova. Aqui, oferecemos acesso fácil e rápido às provas e gabaritos de matemática do Encceja, para que você possa estudar com confiança e se sentir seguro no dia da prova. Não perca mais tempo, prepare-se agora para a prova de matemática do Encceja e alcance seus objetivos.
Prova II - Manhã Matemática
QUESTÃO 31 - Uma criança, viajando de carro com o pai, pergunta como se lê o número “200” junto com a letra “m” na placa que se observa na figura.
Com base nas informações da placa, o pai responde que “200” e “m”, juntos, querem dizer
A) duzentos miligramas.
B) duzentos metros.
C) duzentos milímetros.
D) duzentos minutos.
QUESTÃO 32 - O edital de um processo seletivo abre 30 vagas para diversos cargos. Encerradas as inscrições, a razão candidato/vaga era de 28 por 1. Para a aplicação das provas, serão utilizadas salas de aula nas quais as carteiras serão etiquetadas com os nomes dos candidatos. Foi definido pela comissão organizadora que cada sala precisa ter exatamente 56 carteiras, contando que todos os candidatos estejam presentes para fazer a prova. Pretende-se que a escola mais adequada a esse propósito tenha o menor número de salas, compatível com a exigência dessa comissão. Para isso, a comissão organizadora dispõe de uma tabela com quatro escolas, as quais possuem o número desejado de carteiras por sala.
A escola escolhida pela comissão organizadora será a
A) I.
B) II.
C) III.
D) IV.
QUESTÃO 33 - Um pedreiro precisa pavimentar, com lajotas quadradas, todo o piso de uma sala. Ele desenhou a vista superior da sala em um papel quadriculado, no qual cada quadradinho da malha representa uma lajota, como mostra a figura.
A loja onde ele irá comprar as lajotas vende apenas lajotas inteiras, cabendo ao pedreiro recortá-las depois. Além disso, devido ao risco de quebra durante a obra, esse pedreiro comprará 2 peças a mais do que a quantidade necessária para a pavimentação da sala.
Qual a quantidade mínima de lajotas que o pedreiro deve comprar?
A) 18
B) 19
C) 21
D) 23
QUESTÃO 34 - Artur recebe R$ 2 000,00 de salário mensal e decidiu agendar uma reunião com seu chefe para negociar um reajuste salarial.
O índice mínimo de reajuste que ele deve negociar para que seu salário passe a ser, no mínimo, de R$ 2 500,00 é
A) 20%
B) 25%
C) 50%
D) 125%
QUESTÃO 35 - Uma colcha de retalhos, com formato retangular, é feita com quatro recortes triangulares de tecidos, conforme a figura.
Considere que as costuras nos sentidos das diagonais dessa colcha são perfeitamente retilíneas.
O retalho A da colcha, que tem o formato de um triângulo, pode ser classificado quanto a seus ângulos internos e lados, respectivamente, como
A) acutângulo e equilátero.
B) obtusângulo e escaleno.
C) obtusângulo e isósceles.
D) retângulo e isósceles.
QUESTÃO 36 - A cor dos pelos nas cobaias é condicionada por uma série de fatores genéticos. Uma cobaia marrom teve três ninhadas, cada uma com um macho diferente. O quadro seguinte mostra a constituição de cada ninhada.
Escolhendo um descendente marrom ao acaso, a probabilidade de ele ser da 2ª ninhada é
A) 8/27
B) 1/3
C) 4/9
D) 1/2
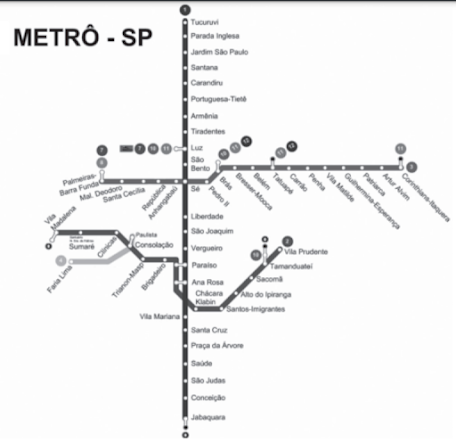
QUESTÃO 37 - Paulo precisa localizar sua amiga Juliana, que está em alguma estação do metrô de São Paulo. Para isso, usará o mapa do metrô representado na figura. Juliana disse apenas que pegou o metrô na estação Portuguesa-Tietê no sentido Jabaquara e desceu na 3ª estação após a estação São Bento.
Na figura, cada ponto branco próximo ao nome da estação indica a sua posição. Mapa do metrô de São Paulo. Disponível em: www.viajenodetalhe.com.br. Acesso em: 9 set. 2013.
A estação em que Juliana está é
A) Luz.
B) Armênia.
C) São Joaquim.
D) Jardim São Paulo.
QUESTÃO 38 - Um torcedor, antes de acessar as instalações de um estádio, comprou uma bebida cujo vasilhame de vidro traz no seu rótulo a informação: “Conteúdo líquido: 320 mL”. Não podendo acessar o estádio com esse vasilhame, ele deverá passar toda a bebida para um copo descartável de plástico em que caiba todo o conteúdo.
Que capacidade mínima deverá ter o copo, em centímetro cúbico, para comportar todo o conteúdo descrito no rótulo?
A) 0,32
B) 3,20
C) 32,00
D) 320,00
QUESTÃO 39 - Uma pessoa deseja comprar um notebook pela internet que custa R$ 1 200,00 e o frete para entrega, R$ 40,00. Ela pagará R$ 200,00 de entrada e o restante, incluindo o frete, em cinco parcelas iguais, sem juros.
O valor de cada parcela, em real, será igual a
A) 208.
B) 200.
C) 248.
D) 240.
QUESTÃO 40 - Um comerciante quer comprar peças de decoração, que custam 3 reais cada uma, para serem revendidas em uma feira de artesanato. Para transportar todas as peças até a feira, o comerciante terá um gasto de 50 reais. Considerando que ele revenda todas as peças, cada uma por 5 reais, o comerciante pretende obter, descontado o frete, um lucro de 250 reais.
Para obter o lucro desejado, a quantidade de peças que o comerciante deverá comprar é
A) 60.
B) 100.
C) 125.
D) 150.
QUESTÃO 41 - Quatro empresas apresentaram orçamentos para a festa de casamento de um casal, para 110 convidados, conforme as descrições seguintes:
• Empresa I: 185 reais por pessoa, estando inclusos buffet, decoração e música.
• Empresa II: 170 reais por pessoa, estando inclusos buffet e decoração, e mais 1 200 reais para a música.
• Empresa III: 140 reais por pessoa para o buffet, 2 600 reais para a decoração e 1 300 reais para a música.
• Empresa IV: 135 reais por pessoa para o buffet, 2 800 reais para a decoração e 1 900 reais para a música.
Esse casal escolheu a empresa que apresentou o menor orçamento.
A escolhida foi a empresa
A) I.
B) II.
C) III.
D) IV.
QUESTÃO 42 - Na construção civil existe uma grande variedade de materiais de acabamento. Em especial, na linha de cerâmica e porcelanato, diversas formas e modelos estão disponíveis no mercado. A figura mostra um ambiente que foi revestido com peças de porcelanato que, por terem a forma de um hexágono regular, encaixam-se perfeitamente em torno do ponto P.
A medida do ângulo interno do hexágono regular, que representa a peça de porcelanato na figura, é
A) 360°
B) 240°
C) 150°
D) 120°
QUESTÃO 43 - Cada um dos quatro vendedores que trabalham em uma revendedora de carros usados conseguiu, em determinado dia, comprar um carro e, logo em seguida, revendê-lo. O gráfico mostra os valores de compra e de venda negociados pelos quatro vendedores.
Qual dos vendedores obteve o maior lucro entre a compra e a venda do carro negociado por ele?
A) 1
B) 2
C) 3
D) 4
QUESTÃO 44 - Uma pessoa pretende comprar um hambúrguer pagando-o por meio de um aplicativo de celular que lhe mostra quatro lojas diferentes que vendem o hambúrguer pretendido. Ela comprará na loja que oferecer o menor preço possível para esse hambúrguer. Sabe-se que, se o pagamento for efetuado em parcela única, os estabelecimentos oferecem um desconto no valor do pedido. O quadro mostra os estabelecimentos encontrados, os preços dos hambúrgueres e os respectivos percentuais de desconto.
Em que estabelecimento a pessoa comprará o hambúrguer?
A) I
B) II
C) III
D) IV
QUESTÃO 45 - Na banca de um determinado feirante encontram-se as seguintes placas de preços:
Uma pessoa chegou à feira com R$ 25,00 e comprou, nessa banca, 2 kg de tomate, 4 kg de batata e 3 kg de cebola. Ela pretende gastar o restante do dinheiro comprando pimentão, mas reservando R$ 2,35 para pegar o ônibus de volta para casa.
A quantidade de pimentão, em quilograma, que essa pessoa conseguirá comprar naquela banca é
A) 2,500.
B) 3,675.
C) 5,000.
D) 8,475.
QUESTÃO 46 - Uma mãe precisa administrar um remédio a seu filho, cuja massa corpórea é de 24 kg. A dosagem desse remédio é baseada na massa corpórea da criança. Esse remédio tem dosagem de 9 mL para crianças com até 5 kg de massa. Para indivíduos com mais de 5 kg de massa, a dosagem, em mililitro, é proporcional à massa corpórea, e o quadro a seguir apresenta as dosagens para algumas massas corpóreas.
A dosagem desse remédio, em mililitro, que a mãe deverá dar ao seu filho é
A) 16.
B) 36.
C) 43.
D) 45.
QUESTÃO 47 - Uma pessoa contratou um jardineiro para cortar o gramado de sua residência. O tempo gasto por esse jardineiro para cortar a grama de uma região de 40 m² foi de 80 minutos. A figura representa o gramado, indicando as regiões onde o trabalho já foi realizado e onde o gramado ainda deve ser aparado.
Considere que o jardineiro mantenha o mesmo ritmo de trabalho no restante do gramado.
Quanto tempo, em minuto, o jardineiro levará para concluir o restante do corte do gramado?
A) 320
B) 200
C) 120
D) 100
QUESTÃO 48 - O sistema de venda de passagens numa empresa de ônibus associa a acomodação de um passageiro no ônibus de acordo com a ordem em que a passagem é vendida. Essa associação segue o seguinte padrão: o primeiro passageiro é associado ao assento 1A, o segundo, ao assento 1B, o terceiro, ao assento 1C, o quarto, ao assento 1D, o quinto, ao assento 2A, e assim sucessivamente. A imagem ilustra uma parte da distribuição dos assentos nos ônibus dessa empresa, os quais têm 12 fileiras horizontais.
Um passageiro comprou a vigésima sétima passagem de um ônibus dessa empresa.
Esse passageiro será associado ao assento
A) 2C.
B) 3C.
C) 6C.
D) 7C.
QUESTÃO 49 - Para ir à casa de seus avós, um menino gasta menos de duas horas utilizando uma linha de ônibus. Um dia, porém, um acidente no trajeto dessa linha de ônibus deixou o fluxo de veículos muito lento e o menino levou 2 ½ horas para completar o mesmo trajeto.
O número decimal correspondente ao tempo, em hora, que o menino gastou para completar o trajeto nesse dia foi
A) 0,5.
B) 1,5.
C) 2,0.
D) 2,5.
QUESTÃO 50 - Um cliente recebeu sua fatura mensal do cartão de crédito no valor de R$ 2 500,00 mas não podia fazer o pagamento integral da fatura. Para quitação do débito de forma parcelada, a administradora do cartão de crédito ofereceu os seguintes planos de pagamento:
• Plano 1: entrada de R$ 900,00 mais uma parcela de R$ 1 800,00.
• Plano 2: entrada de R$ 400,00 mais saldo devedor de R$ 2 100,00 acrescido de juros de 10%.
• Plano 3: entrada de R$ 1 500,00 mais saldo devedor de R$ 1 000,00 acrescido de juros de 15%.
• Plano 4: entrada de R$ 500,00 mais saldo devedor de R$ 2 000,00 acrescido de juros de 9%.
A qual desses planos o cliente deve aderir para ter o menor gasto total com o pagamento dessa fatura?
A) 1
B) 2
C) 3
D) 4
QUESTÃO 51 - O dono de um automóvel bicombustível queria verificar qual combustível lhe proporcionaria menor gasto mensal, considerando que seus deslocamentos diários eram feitos sempre pelos mesmos trajetos. Em cada abastecimento, colocou a mesma quantidade de combustível e anotou o valor pago pelo abastecimento. Posteriormente, calculou a distância percorrida com aquela quantidade de combustível e construiu o seguinte quadro:
O critério de rendimento utilizado por essa pessoa foi observar quanto ela gastava para percorrer cada quilômetro com seu carro, quando abastecido pelos diferentes tipos de combustíveis.
Ordenando os combustíveis pelo seu critério de rendimento, do mais econômico para o menos econômico, o dono do automóvel obteve corretamente a sequência
A) etanol – gasolina comum – gasolina aditivada.
B) gasolina aditivada – gasolina comum – etanol.
C) gasolina comum – etanol – gasolina aditivada.
D) gasolina aditivada – etanol – gasolina comum.
QUESTÃO 52 - Uma pessoa tomou um determinado empréstimo e realizará o pagamento deste em 11 parcelas mensais, iguais e consecutivas, de R$ 1 000,00.
Mas, após pagar 5 dessas parcelas, percebeu que essa despesa mensal correspondia a 40% de seu salário. Para reorganizar suas contas, só poderia arcar com uma parcela que correspondesse a 20%. O seu salário permanecerá igual até o término do empréstimo.
Ao buscar renegociar o montante que ainda iria vencer, recebeu as seguintes propostas calculadas sob juros simples, incidindo sobre o valor que falta pagar e dividindo o pagamento a ser feito em parcelas iguais e consecutivas.
A proposta que se enquadra na condição possível de pagamento dessa pessoa é a
A) I.
B) II.
C) III.
D) IV.
QUESTÃO 53 - Para efetuar a medida de uma grandeza, precisamos estabelecer uma unidade de medida como referência para, a partir daí, definir o comprimento, a área, a massa ou o que se quer medir. Observe a tirinha.
O personagem Caco, a fim de impressionar seu amigo, determinou a sua altura em um submúltiplo do metro, que é a unidade padrão no Sistema Internacional de Unidades para medir a grandeza comprimento. Pode-se considerar que ele não está sendo exagerado, pois a altura média de um animal adulto da sua espécie é de 1,50 m. Com base nessas informações, quantos centímetros devem ser somados à medida da altura de Caco para alcançar a média de altura de um animal adulto de sua espécie?
A) 70
B) 65
C) 7
D) 0,7
QUESTÃO 54 - Uma empresa realiza o transporte de mudanças intermunicipais. Para facilitar o trabalho dos funcionários na elaboração de orçamentos, disponibiliza um quadro que relaciona o preço a ser cobrado com a distância percorrida entre a coleta e a entrega dos objetos. O preço total a pagar (P) é composto por um valor proporcional à quantidade de quilômetros percorridos (d), acrescido de um valor fixo de R$ 400,00, referente ao carregamento e à descarga dos objetos.
A) P = 400 + 3d
B) P = 400 + 10d
C) P = 400d + 3
D) P = 3d + 10
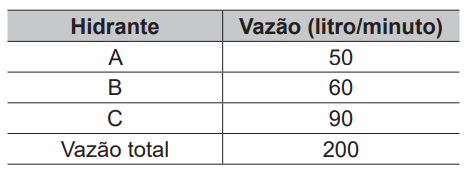
QUESTÃO 55 - O corpo de bombeiros de uma cidade possui três hidrantes para combate a incêndios. A vazão de cada hidrante é apresentada na tabela.
Em função do aumento do número de habitantes e considerando o histórico do número de atendimentos, o comandante do corpo de bombeiros julgou prudente dobrar a vazão total de água nos hidrantes para assegurar o sucesso das operações de combate aos incêndios.
Para esse propósito, as vazões dos hidrantes A e B foram aumentadas ao máximo, para 80 L/min e 100 L/min, respectivamente. Para que a vazão de água dos três hidrantes juntos seja duplicada, a vazão, em litro por minuto, do hidrante C deve ser aumentada para
A) 220.
B) 180.
C) 130.
D) 110.
QUESTÃO 56 - Em um colégio, para que o aluno seja aprovado, ele deve obter, como média aritmética simples das notas dos 4 bimestres, um valor igual ou superior a 60 pontos. Para compor a nota bimestral, são realizados dois trabalhos, cada um valendo T pontos, três provas, cada uma valendo P pontos, e um seminário valendo S pontos, totalizando 100 pontos essas seis avaliações. As notas obtidas por um aluno nos três primeiros bimestres estão indicadas no quadro.
Esse aluno calculou a nota mínima necessária para que seja aprovado.
A expressão algébrica que relaciona os valores a serem obtidos nas avaliações do 4º bimestre, de forma a garantir a nota mínima necessária para que esse aluno seja aprovado, é
A) T + P + S = 60
B) 2T + 3P + S = 60
C) 2T + 3P + S = 80
D) 2T + 3P + S = 100
QUESTÃO 57 - Dois amigos, A e B, fizeram uma brincadeira: a cada número x, dito pelo amigo A, o amigo B respondia com um valor y, que seguia uma regra criada por ele. O objetivo da brincadeira era o amigo A descobrir a regra criada pelo amigo B.
Os valores observados em cada rodada dessa brincadeira estão representados no quadro.
A expressão que representa a regra criada pelo amigo B, a partir do número x, é igual a
A) x + 3
B) 3x – 1
C) x – 3
D) 3x + 1
QUESTÃO 58 - Em uma escola, foram comprados 120 m de tela. Toda essa tela deverá ser usada para cercar duas regiões quadradas: um galinheiro e uma horta. A fim de evitar que as aves comam as hortaliças, o galinheiro e a horta não terão fronteiras em comum. A direção da escola quer que a soma das áreas das duas regiões seja a maior possível, sendo que o lado do galinheiro deve medir, pelo menos, 14 m, enquanto o lado da horta deve medir, pelo menos, 13 m.
Suponha que, além disso, deseja-se que os comprimentos dos lados de ambas as regiões sejam números inteiros.
Qual deverá ser a medida, em metro, do lado do galinheiro para se atingir esse objetivo?
A) 14
B) 15
C) 16
D) 17
QUESTÃO 59 - Um jardineiro foi contratado para colocar grama em um terreno. No primeiro dia, ele colocou grama em metade do terreno, deixando o restante para fazer posteriormente. No segundo dia, chegou atrasado ao trabalho e colocou grama apenas na metade da parte que restou sem grama após o primeiro dia.
A fração que representa a parte do terreno que ainda está sem grama após esses dois dias de trabalho é
A) 1/3
B) 2/3
C) 1/4
D) 3/4
QUESTÃO 60 - A crise hídrica vivida recentemente no Brasil trouxe para as manchetes dos jornais os níveis dos reservatórios de água brasileiros. Nas imagens a seguir há uma ilustração do que são o volume útil e o volume morto de um reservatório de água, além dos níveis dos reservatórios que abastecem o estado do Rio de Janeiro, referentes ao dia 13 de agosto de 2015.
O reservatório de Santa Branca tem capacidade para armazenar 438,5 bilhões de litros de água. O volume morto desse reservatório é de 131,2 bilhões de litros de água e representa 29,92% de sua capacidade.
O volume útil de água disponível no reservatório Santa Branca, no dia 13 de agosto de 2015, em bilhões de litros, era mais próximo de
A) 9,83.
B) 43,10.
C) 122,15.
D) 174,30.
GABARITO - Prova II - Manhã Matemática - Ensino Fundamental
31) B
32) B
33) C
34) B
35) C
36) B
37) C
38) D
39) A
40) D
41) C
42) D
43) B
44) A
45) A
46) B
47) A
48) D
49) D
50) C
51) C
52) D
53) A
54) A
55) A
56) C
57) B
58) D
59) C
60) B