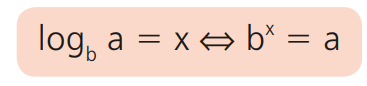A palavra "juros" é comumente encontrada em diversos meios de comunicação no nosso dia a dia. Algumas situações comuns incluem: tomar um empréstimo em um banco, atrasar o pagamento de uma conta de consumo, abrir uma caderneta de poupança e ultrapassar o limite de cheque especial. Nessas operações, geralmente é estabelecida uma taxa de juros (x por cento) por período (dia, mês, ano) que incide sobre o valor da transação.
Em Matemática Financeira, alguns termos comuns são: unidade monetária (real, dólar, euro, etc.), capital (valor inicial de um empréstimo, dívida ou investimento), taxa de juros (expressa como percentual por período), juros (valor obtido ao aplicar a taxa sobre o capital ou outro valor da transação) e montante (capital acrescido dos juros auferidos na transação). Para o período de um mês, é adotado o chamado mês comercial com 30 dias.
Juros simples: uma explicação detalhada e exemplos práticos
Os juros simples são uma forma de remuneração pelo uso de dinheiro emprestado. Eles são calculados sobre o valor do capital inicial e não levam em conta os juros acumulados ao longo do tempo.
O cálculo dos juros simples é feito através da seguinte fórmula: juros = capital x taxa x tempo.
J= Cit
A taxa é expressa em porcentagem e o tempo em períodos (dias, meses, anos).
Exemplo: Se um indivíduo empresta R$1000,00 a uma taxa de juros de 10% ao mês por 3 meses, os juros simples seriam calculados da seguinte forma: juros = 1000 x 0,10 x 3 = R$300,00.
Os juros simples são comumente utilizados em transações financeiras como empréstimos pessoais, cartões de crédito e empréstimos para pequenas empresas. Eles também são utilizados em investimentos de renda fixa, como CDBs e títulos públicos, onde o rendimento é calculado sobre o capital investido.
É importante notar que os juros simples não levam em conta a acumulação dos juros ao longo do tempo, o que pode resultar em menor rendimento quando comparado aos juros compostos. Por essa razão, é importante avaliar cuidadosamente as opções de investimento e empréstimo antes de escolher uma que seja adequada às suas necessidades financeiras.
Em resumo, os juros simples são uma forma de remuneração pelo uso de dinheiro emprestado, calculado sobre o capital inicial e sem levar em conta os juros acumulados ao longo do tempo. Eles são comumente utilizados em transações financeiras e investimentos de renda fixa, mas devem ser avaliados cuidadosamente antes de serem escolhidos devido a seus rendimentos menores comparado aos juros compostos.
Juros compostos: o segredo por trás do crescimento exponencial
Juros compostos são a forma mais comum de juros encontrada em operações financeiras, como empréstimos, investimentos e poupanças. A principal diferença entre juros simples e compostos é que, no segundo caso, os juros gerados a cada período são adicionados ao capital, e assim, os juros dos períodos seguintes incidem sobre um valor cada vez maior. Para entender como funcionam os juros compostos, vamos usar como exemplo um investimento de R$1.000,00 a uma taxa de juros de 10% ao ano. Após o primeiro ano, o valor do investimento seria de R$1.100,00 (R$1.000,00 + R$100,00 de juros). No segundo ano, a taxa de juros seria aplicada sobre R$1.100,00, gerando juros de R$110,00 e um montante final de R$1.210,00. É fácil notar como, ao longo do tempo, os juros compostos geram um acúmulo de valor muito maior do que os juros simples. Em nosso exemplo, após 10 anos, o montante final seria de R$2.594,87, enquanto que, se fossem juros simples, seriam R$2.000,00. Além disso, os juros compostos também são utilizados em operações de empréstimo, onde o devedor deve pagar juros sobre o valor devido, incluindo os juros anteriores. Isso pode levar a uma situação de dívida crescente e difícil de ser quitada.
A fórmula dos Juros Compostos
É importante lembrar que, quanto maior for a taxa de juros e o período de tempo, maior será o acúmulo de juros compostos. Por isso, é fundamental avaliar cuidadosamente as taxas de juros e prazos antes de fazer qualquer investimento ou contratar um empréstimo. Em resumo, os juros compostos são uma forma de juros mais comum e eficiente para quem deseja investir e acumular dinheiro ao longo do tempo, mas é necessário estar ciente de sua dinâmica e de como ela pode afetar as operações financeiras.
Exemplos práticos de cálculo de juros simples e compostos
1 - Juros simples: Um empréstimo de R$ 1.000,00 a uma taxa de juros de 10% ao ano, por 1 ano.
Solução: Juros = C x i x t = 1.000 x 0,1 x 1 = R$ 100,00. Montante = C + J = 1.000 + 100 = R$ 1.100,00
2 - Juros compostos: Um investimento de R$ 1.000,00 a uma taxa de juros de 10% ao ano, por 1 ano.
Solução: Montante = C (1 + i)^t = 1.000 (1 + 0,1)^1 = R$ 1.100,00
3 - Juros simples: Um empréstimo de R$ 10.000,00 a uma taxa de juros de 5% ao mês, por 6 meses.
Solução: Juros = C x i x t = 10.000 x 0,05 x 6 = R$ 3.000,00. Montante = C + J = 10.000 + 3.000 = R$ 13.000,00
4 - Juros compostos: Um investimento de R$ 5.000,00 a uma taxa de juros de 7% ao mês, por 6 meses.
Solução: Montante = C (1 + i)^t = 5.000 (1 + 0,07)^6 = R$ 8.872,73
5 - Juros simples: Um empréstimo de R$ 20.000,00 a uma taxa de juros de 2% ao dia, por 90 dias.
Solução: Juros = C x i x t = 20.000 x 0,02 x 90 = R$ 3.600,00. Montante = C + J = 20.000 + 3.600 = R$ 23.600,00
6 - Juros compostos: Um investimento de R$ 15.000,00 a uma taxa de juros de 0,5% ao dia, por 90 dias.
Solução: Montante = C (1 + i)^t = 15.000 (1 + 0,005)^90 = R$ 17.928,58
Relembrando:
- Dados os números reais a e b, a > 0 e 0 < b e b ≠ 1, chama-se logaritmo de a na base b (indica-se logb a) o número real x tal que b^x = a:
lembre-se de que, quando a base é omitida, convenciona-se que ela é igual a 10, ou seja, é o logaritmo decimal.
| Propriedade | Explicação |
|---|---|
| log(a*b) = log(a) + log(b) | A soma dos logaritmos é igual ao logaritmo do produto |
| log(a/b) = log(a) - log(b) | A diferença dos logaritmos é igual ao logaritmo do quociente |
| log(a^n) = n*log(a) | O logaritmo de uma potência é igual ao expoente multiplicado pelo logaritmo da base |
| log(1) = 0 | O logaritmo de 1 é sempre 0 |
| log(a) = log(e^(log(a))) | O logaritmo de um número é igual ao logaritmo natural da sua exponenciação |
| log(a) é um número real quando a > 0 e a ≠ 1 | Logaritmos só são reais quando a base é maior que zero e diferente de 1 |
| log(a) é um número negativo quando 0 < a < 1 | Logaritmos são negativos quando a base está entre 0 e 1 |
| log(a) é um número positivo quando a > 1 | Logaritmos são positivos quando a base é maior que 1 |
| log(a) é uma função crescente quando a > 0 | Logaritmos aumentam quando a base aumenta |
| log(a) é uma função inversa da exponenciação | log(a^b) = b e a^log(b) = b |
Juros Simples e Compostos:
| Tipo | Explicação | Fórmula |
|---|---|---|
| Juros Simples | Os juros são calculados somente sobre o montante principal | J = P * i * n |
| Juros Compostos | Os juros são calculados sobre o montante principal e sobre os juros acumulados | M = P(1+i)^n |
- P = montante principal
- i = taxa de juros
- n = período de tempo
- J = juros
- M = montante final (montante principal + juros)
Em resumo, os juros simples são calculados somente sobre o montante inicial, enquanto os juros compostos são calculados sobre o montante inicial e sobre os juros acumulados, o que os torna mais vantajosos ao longo do tempo.