Conjuntos Numéricos - Matemática
A Origem dos números
Os números nem sempre foram grafados como os conhecemos atualmente. Eles percorreram uma longa história e foram organizados pouco a pouco, ao longo de milênios, em diferentes culturas, sempre na busca de representar e manipular quantidades.
Descobertas históricas evidenciam registros com riscos em ossos e em paredes de cavernas. Registros em placas de argila foram encontrados em sítios arqueológicos do Oriente Médio, correspondendo a um período que se estende de 9 000 a 2 000 anos antes da nossa era.
Há mais de 5 000 anos, sociedades avançadas, que precisavam realizar diferentes operações econômicas e em grande quantidade, não podiam mais confiar tantos dados apenas à memória humana. Assim, acredita-se que surgiu a ideia de representar as quantidades por meio de sinais gráficos. A seguir, é possível observar os símbolos utilizados nos sistemas de numeração de algumas civilizações e os algarismos como conhecemos atualmente, chamados de indo-arábicos.
Números Naturais (N)
O conjunto dos números naturais é representado pela letra ℕ
O conjunto dos números naturais é infinito: para qualquer número natural, sempre podemos ter um sucessor maior que ele. O sucessor de um número natural b é o número ( b + 1 ) . Definimos também o antecessor de um número natural b, b ≠ 0 , como sendo o número ( b - 1 ).
Números Inteiros (Z)
Os números inteiros foram negados como números até o século XVIII. Apesar de diversos matemáticos terem se deparado com números negativos em operações e até mesmo na resolução de equações, sempre que isso acontecia o problema era classificado como impossível ou absurdo.
Hoje, o uso desses números é frequente em diversas situações cotidianas, como nas relacionadas a operações financeiras ou mesmo para indicar medidas de temperaturas.
Como os números naturais, os números inteiros também são ordenados: uma vez que, dados dois números inteiros quaisquer, é sempre possível dizer se eles são iguais ou se um é menor ou maior que o outro.
Podemos destacar os seguintes subconjuntos de ℤ:
Números Racionais (Q)
A origem dos números racionais positivos é milenar. No entanto, pela ausência da escrita ou de qualquer outra forma de registro, o que sabemos é que ela surgiu por volta do ano 3000 a.C., por causa de um problema relacionado ao controle das propriedades de terras às margens do rio Nilo, no Egito.
Ao medir as terras às margens do rio Nilo, os egípcios perceberam que nem sempre o resultado da medição correspondia a um número inteiro de vezes da unidade utilizada. Assim, tendo em vista que os números inteiros eram insuficientes para exprimir as medidas desejadas, eles criaram os números fracionários.

Do mesmo modo,

Além disso, observe que todo número inteiro é um número racional, pois ele pode ser escrito na forma fracionária. Veja dois exemplos.
Uma fração, em sua origem, corresponde à divisão de um inteiro em partes iguais. Essa ideia pode ser estendida para qualquer inteiro.
Observe abaixo o inteiro representado por um quadrado de área 25 e as figuras seguintes, que representam frações desse inteiro.
O período de uma dízima é o algarismo, ou o grupo de algarismos, que se repete na dízima periódica. No caso das divisões acima, temos:
PROBLEMAS E EXERCÍCIOS RESOLVIDOS
01 - Dizemos que uma fração é irredutível quando ela não pode ser simplificada. Com base nessa informação, obtenha a fração irredutível equivalente a cada decimal exato a seguir.
a) 0,7
b) 2 0182
c) 1,95
d) 0,02
Resolução
02 - Obtenha a fração irredutível equivalente a cada dízima periódica.
a) 0,232323…
b) 3,666...
03 - Uma dízima periódica, representada na forma decimal, é chamada de composta quando, antes dos números que se repetem, aparecem algarismos que não fazem parte do período. Por exemplo, na dízima 0,2171717... 17 é o período e 2 é chamado de anteperíodo.
Com base nessa informação, obtenha a fração irredutível equivalente a cada dízima periódica composta.
a) 0,2171717…
b) 0,35111…

NÚMEROS REAIS (R)
Quando falamos em números reais, estamos abrangendo todos os números vistos até aqui, ou seja, os números reais resultam da união dos números racionais com os irracionais.Reta real
- Escolher um ponto sobre a reta que represente o zero ou a origem
- Estabelecer dois sentidos: um positivo e um negativo
- Escolher uma unidade de medida para graduar a reta.





















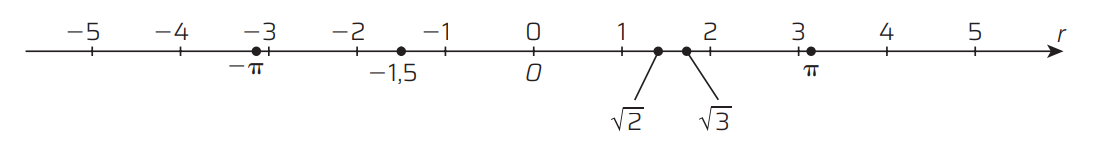


Comentários
Postar um comentário