No vasto campo da matemática, a função afim emerge como uma ferramenta fundamental para modelar relações lineares entre variáveis. Dois elementos-chave que delineiam o comportamento desta função são o coeficiente linear e o coeficiente angular. Neste artigo, vamos desbravar as engrenagens da função afim, compreendendo a influência do coeficiente linear e do coeficiente angular, e como esses elementos são cruciais na representação gráfica e na interpretação das relações matemáticas.
Entendendo a Função Afim
A função afim tem a forma geral f(x) = mx + b, onde m é o coeficiente angular e b é o coeficiente linear. Essa equação descreve uma linha reta no plano cartesiano e é a espinha dorsal para modelar uma variedade de situações do mundo real.
Coeficiente Angular m: A Inclinação da Reta
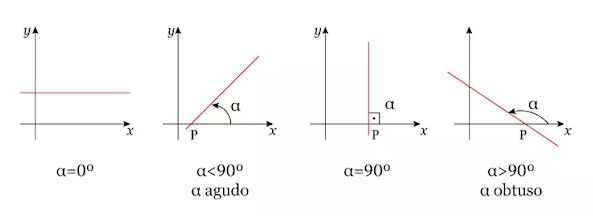
O coeficiente angular m é a medida da inclinação da reta. Ele indica o quanto a função está "subindo" ou "descendo". Se m > 0, a função é crescente; se m < 0, é decrescente. Um m igual a zero resulta em uma linha horizontal. Quanto maior o valor absoluto de m, mais íngreme é a inclinação.
Coeficiente Linear b: O Ponto de Interseção com o Eixo y
O coeficiente linear b é o ponto onde a reta intersecta o eixo y. Em outras palavras, quando x = 0, f(x) = b. O valor de b determina a posição vertical da reta no plano cartesiano. Uma função afim com b = 0 passa pela origem.
Representação Gráfica: A Importância da Visualização
A representação gráfica de uma função afim fornece insights valiosos. O coeficiente angular determina a inclinação da reta, enquanto o coeficiente linear define a posição inicial no eixo y. Juntos, eles moldam a aparência e o comportamento da função no plano cartesiano.
Aplicações Práticas: Modelando Relações do Mundo Real
As funções afins, com seus coeficientes linear e angular, encontram aplicações em diversos campos:
1. Economia: Modelagem de custos e receitas em negócios.
2. Física: Descrição de movimentos uniformes e acelerados.
3. Engenharia: Análise de sistemas lineares em circuitos elétricos.
Interpretação Numérica e Geométrica: Uma Dupla Perspectiva
A interpretação numérica dos coeficientes oferece insights sobre as taxas de variação e valores iniciais, enquanto a interpretação geométrica destaca como esses coeficientes se traduzem visualmente na inclinação e posição da reta.
Desafios e Exploração Adicional: Aprimorando Habilidades Analíticas
Desafie-se a resolver problemas que envolvam funções afins, ajustando os coeficientes para observar as mudanças resultantes. Isso aprimora a compreensão prática da influência dos coeficientes.
Conclusão: Os Eixos Mestres da Função Afim
Ao explorar os coeficientes linear e angular da função afim, desvendamos os eixos mestres que definem seu comportamento. Esses coeficientes não apenas moldam a aparência gráfica da função, mas também oferecem insights valiosos sobre relações matemáticas e modelagem do mundo real. Ao compreender a influência única de cada coeficiente, abrimos as portas para uma apreciação mais profunda das nuances matemáticas por trás da função afim.
Saiba mais sobre A Função Polinomial do 1º Grau
Raiz de uma Função Polinomial do 1º Grau
Coeficiente Linear e Coeficiente Angular