Potenciação e Radiciação

byAdriano Rocha -
0

 A potenciação ou exponenciação é a operação matemática que representa a multiplicação de fatores iguais. Ou seja, usamos a potenciação quando um número é multiplicado por ele mesmo várias vezes.

Para escrever um número na forma de potenciação usamos a seguinte notação:

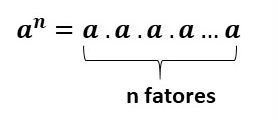
potenciação

Sendo a ≠ 0, temos:

a: Base (número que está sendo multiplicado por ele mesmo)
n: Expoente (número de vezes que o número é multiplicado)

Para melhor entender a potenciação, no caso do número 23 (dois elevado a terceira potência ou dois elevado ao cubo), tem-se:

23 = 2 x 2 x 2 = 4 x 2 = 8

Sendo,

2: Base
3: Expoente
8: Potência (resultado do produto)

Exemplos de Potenciação

52: lê-se 5 elevado à segunda potência ou 5 ao quadrado, donde:

5 x 5 = 25

Logo,

A expressão 52 equivale a 25.

33: lê-se 3 elevado à terceira potência ou 3 ao cubo, donde:

3 x 3 x 3 = 27

Logo,

A expressão 33 equivale a 27.

Potenciação (exponenciação): o que é e propriedades das

Radiciação é a operação que realizamos quando queremos descobrir qual o número que multiplicado por ele mesmo determinada quantidade de vezes, dá um valor que conhecemos.

Exemplo: Qual é o número que multiplicado por ele mesmo 3 vezes dá como resultado 125?

Por tentativa podemos descobrir que:

5 x 5 x 5 = 125, ou seja, 5 ao cubo espaço igual a espaço 125

Escrevendo na forma de raiz, temos:

cúbica raiz de 125 espaço igual a espaço 5

Portanto, vimos que o 5 é o número que estamos procurando.

Símbolo da Radiciação

Para indicar a radiciação usamos a seguinte notação:

negrito n enésima raiz de negrito x

Sendo,

n o índice do radical. Indica quantas vezes o número que estamos procurando foi multiplicado por ele mesmo.
x o radicando. Indica o resultado da multiplicação do número que estamos procurando por ele mesmo.

Exemplos de radiciação:

raiz quadrada de 400(Lê-se raiz quadrada de 400)

cúbica raiz de 27 (Lê-se raiz cúbica de 27)

quinta raiz de 32 (Lê-se raiz quinta de 32)

Propriedades da Radiciação

1ª propriedade:

reto n enésima raiz de reto a à potência de reto m fim da raiz espaço igual a espaço reto a à potência de tipográfico reto m sobre reto n fim do exponencial

Já que a radiciação é a operação inversa da potenciação, todo radical pode ser escrito na forma de potência.

Exemplo: quinta raiz de 4 ao cubo fim da raiz espaço igual a espaço 4 à potência de tipográfico 3 sobre 5 fim do exponencial

2ª propriedade:

reto n enésima raiz de reto a à potência de reto m fim da raiz espaço igual a espaço índice radical reto n. reto p de reto a à potência de reto m. reto p fim do exponencial fim da raiz espaço reto n enésima raiz de reto a à potência de reto m fim da raiz espaço igual a espaço índice radical reto n dividido por reto p de reto a à potência de reto m dividido por reto p fim do exponencial fim da raiz

Multiplicando-se ou dividindo-se índice e expoente pelo mesmo número, a raiz não se altera.

Exemplos:

índice radical espaço em branco de 16 espaço igual a índice radical espaço em branco de 2 à potência de 4 fim da raiz igual a espaço índice radical 2.2 de 2 à potência de 4.2 fim do exponencial fim da raiz espaço igual a espaço quarta raiz de 2 à potência de 8 fim da raiz espaço igual a espaço quarta raiz de 256 espaço igual a 4

quarta raiz de 256 espaço igual a quarta raiz de 2 à potência de 8 fim da raiz igual a espaço índice radical 4 dividido por 2 de 2 à potência de 8 dividido por 2 fim do exponencial fim da raiz igual a índice radical espaço em branco de 2 à potência de 4 fim da raiz igual a raiz quadrada de 16 espaço igual a espaço 4

3ª propriedade:

reto n enésima raiz de reto a. reto n enésima raiz de reto b espaço igual a espaço reto n enésima raiz de reto a. reto b fim da raiz numerador reto n enésima raiz de reto a sobre denominador reto n enésima raiz de reto b fim da fração igual a espaço reto n enésima raiz de reto a sobre reto b fim da raiz vírgula espaço sendo espaço reto b espaço não igual 0

Na multiplicação ou divisão com radiciais de mesmo índice realiza-se a operação com os radicandos e mantém-se o índice do radical.

Exemplos:

cúbica raiz de 9 espaço. espaço cúbica raiz de 3 espaço igual a espaço cúbica raiz de 9.3 fim da raiz espaço igual a espaço cúbica raiz de 27 espaço igual a espaço 3

numerador índice radical espaço em branco de 27 sobre denominador índice radical espaço em branco de 3 fim da fração espaço igual a espaço índice radical espaço em branco de 27 sobre 3 fim da raiz espaço igual a espaço índice radical espaço em branco de 9 espaço igual a espaço 3

4ª propriedade:

abre parênteses reto n enésima raiz de reto a fecha parênteses à potência de reto m espaço igual a espaço reto n enésima raiz de reto a à potência de reto m fim da raiz

A potência da raiz pode ser transformada no expoente do radicando para que a raiz seja encontrada.

Exemplo: parêntese esquerdo índice radical espaço em branco de 2 parêntese direito à potência de 4 espaço igual a espaço índice radical espaço em branco de 2 à potência de 4 fim da raiz espaço igual a raiz quadrada de 16 espaço igual a espaço 4

Quando o índice e a potência apresentam o mesmo valor: parêntese esquerdo reto n enésima raiz de reto a parêntese direito à potência de reto n espaço igual a reto n enésima raiz de reto a à potência de reto n fim da raiz igual a reto a.

Exemplo: parêntese esquerdo quarta raiz de 2 parêntese direito à potência de 4 espaço igual a espaço quarta raiz de 2 à potência de 4 fim da raiz igual a 2

5ª propriedade:

reto n enésima raiz de reto m enésima raiz de reto a fim da raiz espaço igual a espaço índice radical reto n. reto m de reto a

A raiz de outra raiz pode ser calculada mantendo-se o radicando e multiplicando-se os índices.

Exemplo: índice radical espaço em branco de cúbica raiz de 64 fim da raiz espaço igual a espaço índice radical 2.3 de 64 espaço igual a índice radical 6 de 64 espaço igual a espaço 2




Adriano Rocha

Sou professor de matemática com mestrado e experiência em ensinar na escola pública. Ensinar é minha paixão e estou sempre buscando novas formas de tornar a matemática mais acessível e interessante para meus alunos. Se você quer aprender matemática de maneira divertida e desafiadora, venha estudar comigo!

Postar um comentário

Postagem Anterior Próxima Postagem