Teorema de Pitágoras: Formula, conceito e exemplos

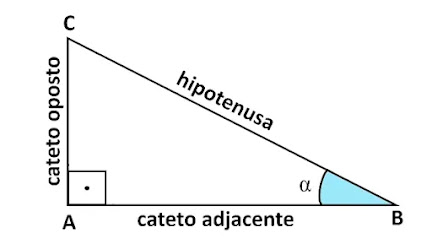
O Teorema de Pitágoras afirma que, em um triângulo retângulo, o quadrado da hipotenusa (o lado oposto ao ângulo reto) é igual à soma dos quadrados dos catetos (os outros dois lados que formam o ângulo reto). Em termos matemáticos, isso pode ser expresso como:

c² = a² + b²

onde "c" representa a hipotenusa e "a" e "b" representam os catetos. Esse teorema é fundamental na geometria e tem aplicações em diversas áreas, como em cálculo, física e engenharia.

Exemplo: Um triângulo retângulo tem um cateto de 3 cm e outro de 4 cm. Qual é o comprimento da hipotenusa?

Solução: Usando o teorema de Pitágoras, temos que c² = a² + b², onde "c" é a hipotenusa e "a" e "b" são os catetos. Substituindo os valores, temos:

c² = 3² + 4²

c² = 9 + 16

c² = 25

c = 5

Portanto, o comprimento da hipotenusa é 5 cm.

Exemplo: Um poste de 6 metros de altura é sustentado por um cabo de aço preso no topo do poste e fixado no solo a uma distância de 8 metros da base do poste. Qual é o comprimento do cabo de aço?

Solução: Este é um exemplo de um triângulo retângulo que envolve um objeto vertical (o poste) e um objeto horizontal (o solo). A altura do poste é um dos catetos, e a distância da base do poste ao ponto onde o cabo toca o solo é o outro cateto. Portanto, usando o teorema de Pitágoras, temos:

c² = 6² + 8²

c² = 36 + 64

c² = 100

c = 10

Portanto, o comprimento do cabo de aço é de 10 metros.

Exemplo: Um quadrado de lado 6 cm é cortado ao meio, formando dois triângulos retângulos. Qual é o comprimento da hipotenusa de um desses triângulos?

Solução: Quando um quadrado é cortado ao meio ao longo de sua diagonal, formam-se dois triângulos retângulos congruentes. Cada um desses triângulos tem um dos lados iguais ao lado do quadrado, que neste caso é 6 cm. Usando o teorema de Pitágoras, temos:

c² = 6² + 6²

c² = 36 + 36

c² = 72

c ≈ 8,485

Portanto, o comprimento da hipotenusa é de cerca de 8,485 cm (arredondando para três casas decimais).