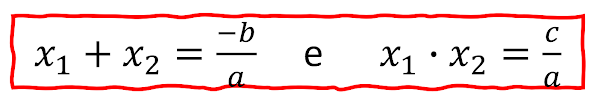A resolução de equações do segundo grau é uma das tarefas mais fundamentais na matemática elementar. Como essas equações aparecem em muitas áreas diferentes da matemática, é importante ter um método prático e eficaz para resolvê-las. Saber como resolver equações do segundo grau é fundamental para o entendimento de muitos conceitos matemáticos e científicos, além de ser uma habilidade importante na vida cotidiana. Ter um método prático para resolver essas equações pode ajudar a simplificar cálculos, tornar a resolução de problemas mais eficiente e aumentar a compreensão dos conceitos matemáticos subjacentes.
Entendendo o método da soma e do produto para resolver equações do segundo grau
O método da soma e do produto é uma técnica utilizada para resolver equações do segundo grau, que é baseada nas propriedades das raízes da equação. Seja a equação do segundo grau na forma padrão
onde a, b e c são constantes, o método da soma e do produto afirma que as raízes da equação podem ser encontradas a partir da soma e do produto dessas constantes.
De maneira mais específica, o método da soma e do produto estabelece que as raízes da equação podem ser representadas como x¹ e x², e que essas raízes estão relacionadas às constantes da equação através das seguintes fórmulas:
Assim, para resolver uma equação do segundo grau usando o método da soma e do produto, basta calcular a soma e o produto das constantes da equação e, em seguida, utilizar as fórmulas acima para determinar as raízes da equação. Esse método é especialmente útil quando as raízes da equação não são facilmente identificáveis por outros métodos, como a fatoração.
Veja o passo a passo do método prático de resolução de equações quadráticas
Seja a equação do segundo grau abaixo
Depois utilize o método - Solteiro (ST) Pega Muito (PM)
- ST - SOMA TROCA O SINAL
- PM - PRODUTO MANTÊM O SINAL
Agora precisamos encontrar dois números x¹ e x² onde a sua soma da -3 e o seu produto da -18
Desse modo, a solução do problema proposto é 1 e -2.
Teste seu conhecimento do esse simulado
---😉Deixe suas dúvidas ou sugestões nos comentários😉---
Pratique o método da soma e do produto com estes 20 exercícios de equações do segundo grau.
1) x² - 5x + 6 = 0 (R: 2, 3)
2) x² - 8x + 12 = 0 (R: 2, 6)
3) x² + 2x - 8 = 0 (R: 2, -4)
4) x² - 5x + 8 = 0 (R: vazio)
5) 2x² - 8x + 8 = 0 (R: 2,)
6) x² - 4x - 5 = 0 (R: -1, 5)
7) -x² + x + 12 = 0 (R: -3, 4)
8) -x² + 6x - 5 = 0 (R: 1, 5)
9) 6x² + x - 1 = 0 (R: 1/3 , -1/2)
10) 3x² - 7x + 2 = 0 (R: 2, 1/3)
11) 2x² - 7x = 15 (R: 5, -3/2)
12) 4x² + 9 = 12x (R: 3/2)
13) x² = x + 12 (R: -3 , 4)
14) 2x² = -12x - 18 (R: -3 )
15)x²-x-20=0 {R:-4 e 5}
16) x²-3x +4 {R:-1 e 4}
17) x²-14x+48=0 {R: 6 e 8}
18) x²+3x-28=0 {R:-7 e 4}
19) x² + 9 = 4x (R: vazio)
20) 25x² = 20x – 4 (R: 2/5)
21) 2x = 15 – x² (R: 3, -5)
22) x² + 3x – 6 = -8 (R: -1, -2)
23) x² + x – 7 = 5 (R: -4 , 3)
24) 4x² - x + 1 = x + 3x² (R: 1)
25) 3x² + 5x = -x – 9 + 2x² (R: -3)
26) 4 + x ( x - 4) = x (R: 1,4)
27) x ( x + 3) – 40 = 0 (R: 5, -8)
28) x² + 5x + 6 = 0 (R:-2,-3)
29) x² - 7x + 12 = 0 (R:3,4)
31) x² + 5x + 4 = 0 (R:-1,-4)
32) 7x² + x + 2 = 0 (vazio)
33) x² - 18x + 45 = 0 (R:3,15)
34) -x² - x + 30 = 0 (R:-6,5)
35) x² - 6x + 9 = 0 (R:3)
36) (x + 3)² = 1 (R:-2,-4)
37) (x - 5)² = 1 (R:3,7)
38) (2x - 4)² = 0 (R:2)
39) (x - 3)² = -2x² (R:vazio)
40) x² - 3 = 4x + 2 (R: -1,5)
PROBLEMAS COM EQUAÇÃO DO 2° GRAU
1) A soma de um numero com o seu quadrado é 90. Calcule esse numero.
(R: 9 e -10)
2) A soma do quadrado de um número com o próprio número é 12. Calcule esse numero.
(R: 3 e -4)
3) O quadrado menos o dobro de um número é igual a -1. Calcule esse número.
(R: 1)
4) A diferença entre o quadrado e o dobro de um mesmo número é 80. Calcule esse número
(R:10 e -8)
5) O quadrado de um número aumentado de 25 é igual a dez vezes esse número. Calcule esse número
(R: 5)
6) A soma do quadrado de um número com o seu triplo é igual a 7 vezes esse número. Calcule esse número.
(R: 0 e 4)
7) O quadrado menos o quádruplo de um numero é igual a 5. Calcule esse número
(R: 5 e -1)
8) O quadrado de um número é igual ao produto desse número por 3, mais 18. Qual é esse numero?
(R: 6 e -3)
9) O dobro do quadrado de um número é igual ao produto desse numero por 7 menos 3. Qual é esse numero?
(R: 3 e ½)
10) O quadrado de um número menos o triplo do seu sucessivo é igual a 15. Qual é esse numero?
(R: 6 e -3)
11) Qual o número que somado com seu quadrado resulta em 56?
(R:-8 e 7)
12) Um numero ao quadrado mais o dobro desse número é igual a 35. Qual é esse número?
(R: -7 e 5)
13) O quadrado de um número menos o seu triplo é igual a 40. Qual é esse número?
(R: 8 e -5)
14) Calcule um número inteiro tal que três vezes o quadrado desse número menos o dobro desse número seja igual a 40.
(R: 4)
15) Calcule um número inteiro e positivo tal que seu quadrado menos o dobro desse número seja igual a 48.
(R: 8)
16) O triplo de um número menos o quadrado desse número é igual a 2. Qual é esse número?
(R:1 e 2)
17) Qual é o número , cujo quadrado mais seu triplo é igual a 40?
(R:5 , -8)
18) O quadrado de um número diminuido de 15 é igual ao seu dobro. Calcule esse número.
(R: 5 e -3)
19) Determine um número tal que seu quadrado diminuído do seu triplo é igual a 26.
(R: 7 e -4)
20) Se do quadrado de um número, negativo subtraimos 7, o resto será 42. Qual é esse número?
(R: -7)
21) A diferença entre o dobro do quadrado de um número positivo e o triplo desse número é 77. Calcule o número.
(R: 7)
22) Determine dois números ímpares consecutivos cujo produto seja 143.
(R: 11 e 13 ou -11, -13)
23) Um azulejista usou 2000 azulejos quadrados e iguais para revestir 45m² de parede. Qual é a medida do lado de cada azulejo? (R:15 cm)
RESOLUÇÃO DE EQUAÇÕES INCOMPLETAS
Resolver uma equação é determinar todas as suas soluções. Vejamos, através de exemplos,
como se resolvem as equações incompletas do 2° grau
1° CASO – equações da forma ax² + c = 0, (b = 0)
Exemplos:
1) x² - 25 = 0
x² = 25
x = ±√25
x = ±5
logo V = (+5 e -5)
2) 2x² - 18 = 0
2x² = 18
x² = 18/2
x² = 9
x = ±√9
x = ±3
logo V = (-3 e +3)
3) 7x² - 14 = 0
7x² = 14
x² = 14/7
x² = 2
x = ±√2
logo V = (-√2 e +√2)
4) x² + 25 = 0
x² = -25
x = √-25
Nesse caso, a equação não tem soluções reais
EXERCÍCIOS
1) Resolva as seguintes equações do 2° grau
a) x² - 49 = 0 (R: -7 e +7)
b) x² = 1 (R: +1 e -1)
c) 2x² - 50 = 0 (R: 5 e -5)
d) 7x² - 7 = 0 (R: 1 e -1)
e) 5x² - 15 = 0 (R: √3 e -√3)
f) 21 = 7x² (R: √3 e -√3)
g) 5x² + 20 = 0 (R: vazio)
h) 7x² + 2 = 30 (R: 2 e -2 )
i) 2x² - 90 = 8 (R: 7 e -7)
j) 4x² - 27 = x² (R:3 e -3)
k) 8x² = 60 – 7x² (R: 2 e -2)
l) 3(x² - 1 ) = 24 (R: 3 e -3)
m) 2(x² - 1) = x² + 7 (R:3 e -3)
n) 5(x² - 1) = 4(x² + 1) (R:3 e -3)
o) (x – 3)(x + 4) + 8 = x (R:2 e -2)
2° CASO: Equações da forma ax² + bx = 0 (c = 0)
Propriedade: Para que um produto seja nulo é preciso que um dos fatores seja zero .
Exemplos
1) resolver x² - 5x = 0
fatorando x(x – 5) = 0
deixando um dos fatores nulo temos x = 0
e o outro x – 5 = 0 , passando o 5 para o outro lado do igual temos x = 5
logo, V = (0 e 5)
2) resolver: 3x² - 10x = 0
fatorando: x(3x – 10) = 0
deixando um dos fatores nulo temos x = 0
Tendo também 3x – 10 = 0
3x = 10
x = 10/3
logo V= (0 e 10/3)
Observe que, nesse caso, uma das raízes é sempre zero.
EXERCÍCIOS
1) Resolva as seguintes equações do 2° grau.
a) x² - 7x = 0 (R: 0 e 7)
b) x² + 5x = 0 (R: 0 e -5)
c) 4x² - 9x = 0 (R: 0 e 9/4)
d) 3x² + 5x =0 (R: 0 e -5/3)
e) 4x² - 12x = 0 (R: 0 e 3)
f) 5x² + x = 0 (R: 0 e -1/5)
g) x² + x = 0 (R: 0 e -1)
h) 7x² - x = 0 (R: 0 e 1/7)
i) 2x² = 7x (R: 0 e 7/2)
j) 2x² = 8x (R: 0 e 4)
k) 7x² = -14x (R: 0 e -2)
l) -2x² + 10x = 0 (R: 0 e 5)
2) Resolva as seguintes equações do 2° grau
a) x² + x (x – 6) = 0 (R: 0 e 3)
b) x(x + 3) = 5x (R: 0 e 2)
c) x(x – 3) -2 (x - 3) = 6 (R: 0 e 5)
d) (x + 5)² = 25 (R: 0 e -10)
e) (x – 2)² = 4 – 9x (R: 0 e -5)
f) (x + 1) (x – 3) = -3 (R: 0 e 2)
Gabarito
Vamos construir esse gabarito juntos?
Deixe a sua solução nos comentários, se tiver correta eu vou incluir no gabarito.
Bons estudos
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
17)
18)