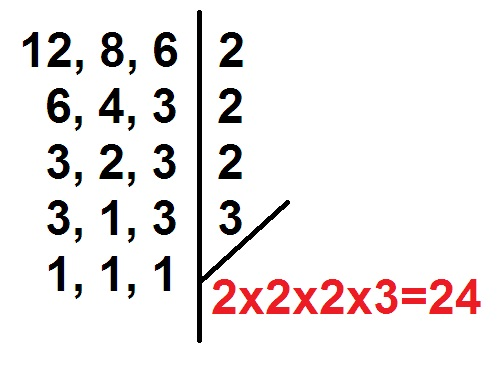Dominando as Operações de Frações: Soma, Subtração, Multiplicando e Dividindo

As frações são um conceito fundamental na matemática e estão presentes em muitas situações do nosso dia a dia. Elas permitem representar quantidades parciais de um todo e são essenciais para resolver problemas que envolvem divisão e proporção. No entanto, operar com frações pode ser desafiador para muitas pessoas, especialmente quando se trata de multiplicação, divisão, soma e subtração. Neste artigo, discutiremos as principais operações com frações e forneceremos exemplos práticos para ajudar os leitores a compreender e dominar esse importante conceito matemático.

Compreendendo o Conceito de Frações: Uma Descrição Completa

Frações são uma forma de representar quantidades parciais de um todo. Elas são compostas por dois números: o numerador e o denominador. O numerador indica a quantidade de partes que se deseja representar e o denominador indica o número total de partes em que o todo foi dividido. Por exemplo, em uma fração como 2/5, o numerador 2 representa duas partes do todo e o denominador 5 indica que o todo foi dividido em cinco partes iguais.

Somando e subtraindo frações com mesmo denominador

Quando as frações têm denominadores iguais, as operações de adição e subtração são simplificadas. Basta manter os denominadores iguais e somar ou subtrair os numeradores correspondentes.

Somando e subtraindo frações com denominadores diferentes

Quando os denominadores são diferentes, é necessário encontrar um denominador comum para realizar operações de frações. Para fazer isso, pode-se encontrar um número que, por meio da multiplicação ou divisão (lembrando que qualquer operação realizada no denominador deve ser feita também no numerador), iguale os denominadores.

Encontrando o MMC pelo Método da Fatoração: Passo a Passo Simples

O método da fatoração é uma técnica eficiente para encontrar o menor múltiplo comum (MMC) de dois ou mais números. Esse método consiste em decompor cada número em fatores primos e, em seguida, multiplicar os fatores primos comuns e não comuns pelo maior expoente encontrado em cada fator. Dessa forma, o resultado será o menor número que é múltiplo de todos os números envolvidos.

Exemplo, encontre o MMC de 12, 8 e 6

Podemos utilizar o método para calcular MMC (minemo múltiplo comum) para somar ou subtrair frações com denominadores diferentes, como segue o exemplo: 

Método da Borboleta: Multiplicando Frações de Forma Simples e Rápida

O método da borboleta, também conhecido como cruzadinha, é uma técnica simples para realizar a multiplicação de frações. A ideia é multiplicar os denominadores para encontrar o valor do denominador da resposta e, em seguida, multiplicar os numeradores cruzadamente.

Para aplicar o método da borboleta, basta multiplicar o denominador da segunda fração pelo numerador da primeira fração, colocando o resultado no numerador da resposta. Em seguida, deve-se manter o sinal da fração e multiplicar o denominador da primeira fração pelo numerador da segunda fração. O resultado dessa multiplicação cruzada ou em formato de borboleta é colocado no denominador da resposta.

Por exemplo, se desejarmos multiplicar as frações 2/3 e 4/5 usando o método da borboleta, devemos multiplicar os denominadores 3 e 5 para encontrar o valor do denominador da resposta (3 x 5 = 15). Em seguida, multiplicamos cruzadamente: 2 x 5 = 10 e 3 x 4 = 12. A resposta é, portanto, 22/15.

Multiplicação de fração

Divisão de fração