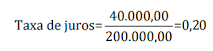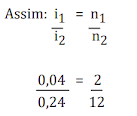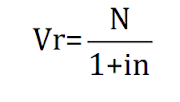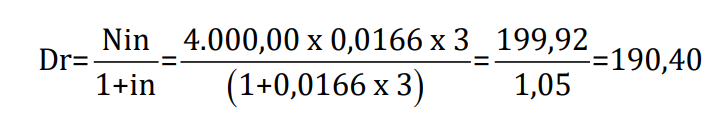O conceito de juros se origina da premissa básica da economia de que os recursos são escassos. A invenção da moeda permitiu que as trocas entre bens fossem realizadas em dinheiro, e com isso surgiu a necessidade de remunerar ou cobrar pelo uso do dinheiro emprestado. De acordo com Mathias e Gomes (2013), juros são definidos como o custo do crédito ou a remuneração de uma aplicação financeira. Quem toma dinheiro emprestado deve pagar juros e quem empresta dinheiro recebe juros. Além disso, as pessoas têm preferencia temporal em consumir ao invés de poupar.
A fórmula utilizada para calcular os juros é:
J = C x i x n,
onde J representa os juros, C representa o capital, i representa a taxa de juros e n representa o prazo de aplicação.
Taxa de juros
Segundo Mathias e Gomes (2013), a Taxa de Juros é determinada por meio de um coeficiente referido a um intervalo de tempo. Este coeficiente corresponde à remuneração do capital empregado por um prazo igual àquele da taxa. A taxa de juros é a relação entre o capital emprestado e o juro devido.
Portanto, conclui-se que taxa de juros é a razão entre os juros (J) e o principal (P) ou capital (C). Simbolicamente, representamos o juro pela letra "i", onde
i = J/P
Onde,
i = corresponde à taxa de juros;
J = representa o juro; e
P = é o valor principal ou presente.
A taxa de juros pode ser apresentada de duas formas, a saber: Em termos percentuais, a mais utilizada em nosso cotidiano, representa o valor pago a cada cem unidades financeiras na unidade de tempo. É o que se obtém depois de dividir o capital por 100.
EXERCÍCIO RESOLVIDO 1 - Um indivíduo tomou R$ 100.000,00 emprestados no banco e pagou R$ 140.000,00 após um ano. Pergunta-se:
a) Quanto foi o juro pago?
b) Qual foi a taxa de juros aplicada nessa operação?
Sabemos que o juro é a diferença entre o que tomamos emprestado e o que pagamos. Assim, temos: R$ 140.000,00 - R$ 100.000,00 = R$ 40.000,00 Temos que encontrar a razão entre o valor pago referente aos juros e o valor do capital. Logo, temos:
Ou em termos percentuais = 20/100 que é igual a 20% a.a
Cálculo do juro
Exemplo: Admita um empréstimo de R$ 2.000,00 em um prazo de dois anos e com taxa de 10% a.a. Qual o valor pago como juro? Resolução: Capital inicial (C) = R$ 2.000,00
Taxa de juros (i) = 10% a.a. Número de períodos (n) = 2 anos Desta forma, temos: J=C×i×n. Logo, J = 2.000,00 x 0,10 x 2 = R$ 400,00
A fórmula básica de juros pode ser descrita de forma algébrica da seguinte forma
Em Matemática Financeira com 03 elementos da fórmula podemos obter o quarto elemento que falta, então geralmente o elemento faltante é o que queremos determinar.
Cálculo do montante
Como vimos anteriormente, o montante é a soma do capital com os juros. Logo, temos a fórmula
M = C + J. Como vimos que J = C x i x n, podemos derivar a fórmula de montante para M = C + Cin. Desta maneira, temos que:
M = C (1+ i n).
Exemplo: Admita um empréstimo de R$ 2.000,00 em um prazo de dois anos e com uma taxa de 10% a.a. Qual o montante após dois anos?
Resolução: Capital inicial (C) = R$ 2.000,00
Taxa de juros (i) = 10% a.a.;
Número de períodos (n) = 2 anos;
M = C (1+in);
M = 2.000,000 (1+ 0,10 x 2) = R$ 2.400,00.
Assim como no caso da fórmula dos juros, a fórmula do montante também apresenta derivações que permitem você encontrar um dos fatores que falta. Volto a repetir que esse fator geralmente é o que se pergunta nas questões.
Taxa proporcional
Conforme Assaf Neto (2012) a compreensão destas taxas exige o reconhecimento de que toda operação envolve dois prazos a saber: (a) o prazo a que se refere a taxa de juros; e (b) o prazo de capitalização de ocorrência dos juros.
Considere duas taxas de juros distintas i1 e i2 relacionadas a dois períodos também distintos n1 e n2. Dizemos que essas taxas são proporcionais se o quociente das taxas e o quociente dos períodos forem iguais:
Exemplo: Verifique se as taxas de 4% ao bimestre e 24% ao ano são proporcionais.
Resolução:
i 1 = 4% a.b. = 0,04 a.b.
i 2 = 24% a.a = 0,24 a.a
n1 = 2 meses
n2 = 12 meses
Temos que são grandezas proporcionais, uma vez que o produto dos meios (0,24 x 2) é igual ao produto dos extremos (0,04 x 12). Conclui-se, portanto, que são taxas proporcionais.
Taxa equivalente
Como saberemos se duas taxas são equivalentes? Aplicamos um mesmo capital às taxas em um mesmo intervalo de tempo; se ambas produzirem o mesmo juro serão consideradas equivalentes. Sejam a taxa de juros i referente ao período 1 e im referente a fração 1/m teoricamente equivalentes. Quando trabalhamos com juros simples, taxas de juros proporcionais são equivalentes.
Exemplo: Suponha um capital de R$ 20.000,00, aplicado de duas formas: 2% a.m. ou 24% a.a., aceitando um prazo de três anos. Verifique se são equivalentes.
Resolução: Aplicando a 2% a.m. em um prazo de três anos (36 meses), temos: J = 20.000,00 x 0,02 x 36 = R$ 14.400,00
Agora aplicando a 24% a.a. em um prazo de três anos (36 meses), temos: J = 20.000,00 x 0,24 x 3 = R$ 14.400,00
Logo, constata-se que o valor pago a título de juros é o mesmo para as duas operações. Concluímos, portanto, que 2% a.m. é equivalente a 24% a.a.
Períodos não-inteiros
Podemos ter situações nas quais o prazo da aplicação (n) não é um número inteiro de período em relação à taxa dada, sendo necessário levar em consideração as frações dos períodos. Nesses casos, temos dois passos a seguir: primeiramente calcula-se o juro da parte inteira do período. Em seguida, calculamos a taxa proporcional à fração de período restante e o juro correspondente. O somatório dos juros será o valor de juro pago nessa operação.
Exemplo: Determine o juro de um capital de R$ 3.000,00, aplicado a uma taxa de 6% ao semestre em um prazo de três anos e nove meses?
Resolução: Como são 3 anos e 9 meses temos 7 semestres (3 anos + 1 semestre + 3 meses). O 1º cálculo é determinar o juro do período inteiro: J1 = 3.000,00 x 0,06 x 7 = 1.260,00 O 2º cálculo é determinar o juro do período não-inteiro: O im representa a taxa equivalente trimestral, pois temos uma taxa semestral (6%a.s.) e queremos encontrar a taxa trimestral, uma vez que 01 semestre tem 02 trimestres.
De tal modo, o total de juros é 1.260,00 + 90,00 = R$ 1.350,00 Sabendo que três meses são iguais a 1/2 semestre, podemos resolver também das seguintes formas: 3.000,00 x 0,06 x 7,5 = R$ 1.350,00.
Juro exato e juro comercial
Geralmente nas operações de curto prazo o regime geralmente adotado é o de juros simples e os prazos são fixados em dias fazendo-se necessário determinar a taxa proporcional referente a 1 dia. Mathias e Gomes (2013) apresentam dois enfoques dependendo do número de dias adotado: (a) ano civil com 365 dias; e (b) ano comercial com 360 dias.
Denomina-se juro exato aquele que é obtido quando o período (n) está disposto em dias e quando isso ocorre, adota-se a convenção de ano civil. Onde:
Já por juro comercial temos aquele que é obtido quando se adota como base o ano comercial. Onde:
Vejamos a diferença no resultado, com o seguinte exemplo:
Determinando a taxa de juros diária (juro exato e juro comercial) a partir de uma taxa anual de 15%. Onde:
Juro exato:
Juro comercial:
O juro comercial diário é superior ao juro exato pelo menor número de dias considerado. No desconto comercial é necessário distinguir a taxa de desconto utilizada na operação e a taxa que efetivamente é cobrada na operação.
Valor nominal, valor atual e valor futuro
Os problemas financeiros dependem basicamente do fluxo do dinheiro no tempo e é mais conhecido na prática por fluxo de caixa. Esse fluxo representa as entradas e saídas de recursos, conforme disposto abaixo. (MATHIAS; GOMES, 2013)
O valor nominal define-se pelo valor de um compromisso na data de seu vencimento, passado o dia de pagamento e o saldo não tenha sido pago o valor nominal permanece e será acrescido os juros e multas acertados na data inicial da operação.
Vejamos a figura abaixo:
Pelo gráfico percebe-se que no 12º mês o valor do capital é de R$ 10.000,00. Ou seja, se um indivíduo aplicou determinada quantia hoje, dada uma taxa de juros, receberá esse valor daqui a 12 meses.Já o valor atual é definido pelo valor de um compromisso antes da data de seu vencimento, para determinar esse valor necessitamos do valor nominal, uma data de cálculo e uma dada taxa de juros para utilização na operação.
Vejamos a figura abaixo:
E por fim temos o valor futuro que é definido pelo valor do título em momento posterior ao que estamos trabalhando.
Vejamos a figura abaixo:
Descontos
Sempre que realiza-se uma operação financeira entre dois ou mais agentes econômicos recebe-se um
documento que comprove a execução da mesma, no geral são entregues títulos de crédito comercial, devendo estes documentos apresentar todas as características da operação, tais como: data da operação,
valor, tipo de operação se à vista ou a prazo. Os títulos mais utilizados nas transações financeiras são:
Nota Promissória, Duplicatas, Recibos, etc.
Segundo Mathias e Gomes (2013) existem dois tipos de desconto: (a) desconto racional ou "por dentro"; e (b) desconto comercial ou "por fora"
O desconto racional é definido como o desconto obtido pela diferença entre o valor nominal e o valor atual de um compromisso, representa em outras palavras a quantia a ser abatida do valor nominal. A fórmula do desconto racional é:
Onde:
N = valor nominal (ou montante);
n = número de períodos antes do vencimento;
i = taxa de desconto;
Dr = valor do desconto;
Vr = valor atual;
Se quisermos obter o valor descontado devemos utilizar a seguinte fórmula:
Exemplo: José pretende saldar um título de R$ 4.000,00, três meses antes de seu vencimento, sabendo-se que a taxa de juros é de 20% a.a., qual será o desconto que ele vai obter?
Resolução: primeiro extraímos as informações disponíveis, depois entendemos o que o exemplo quer dizer, e ai é só resolver. Vamos lá!
N = 4.000,00
n = 3 meses
Calculamos a taxa proporcional, pois temos uma taxa anula e queremos realizar o pagamento três meses antes
O valor do desconto é:
Logo o valor descontado é: R$ 4.000,00 - R$ 190,40 = R$ 3.809,60
O desconto comercial é definido como o valor que se obtém pelo cálculo do juros simples sobre o valor nominal do compromisso a ser quitado antes do seu vencimento. A fórmula do desconto comercial é:
Onde:
N = valor nominal (ou montante);
n = número de períodos antes do vencimento;
i = taxa de desconto;
Dc = desconto comercial;
Vc = valor atual;
Se quisermos obter o valor do desconto devemos utilizar a seguinte fórmula:
Exemplo: José pretende saldar um título de R$ 4.000,00, três meses antes de seu vencimento, sabendo-se que a taxa de juros é de 20% a.a., qual será o desconto que ele vai obter?
Resolução: o desconto comercial é obtido pela aplicação da fórmula. Vamos lá!
Dc = Nin
Dc = 4.000,00 x 0,01666 x 3
Dc = R$ 200,00
O valor do desconto comercial é:
Vc = N (1- in)
Vc = 4.000,00 (1- 0,01666 x 3)
Vc = 4.000,00 x 0,95
Vc = 3.800,00
Perceba o valor obtido no desconto do comercial para o racional. Assim podemos notar no desconto comercial que é necessária a separação entre a taxa de desconto utilizada na operação e a taxa efetivamente cobrada pelo banco. Podemos obter da seguinte forma:
ao trimestre ou 0,208 a.a. em termos percentuais representa 20,8% ao ano.