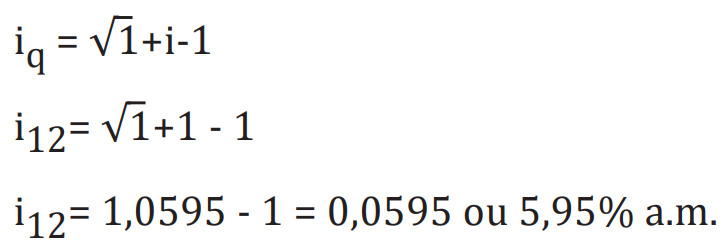No artigo anterior, discutimos sobre os juros simples, que representam um valor calculado com base no valor da dívida e permanecem iguais mês a mês ou ano a ano, dependendo da operação. No entanto, os juros simples raramente são utilizados nas operações financeiras; em vez disso, a maioria das transações usa o regime de juros compostos, que vamos examinar agora com mais detalhes.
Essa modalidade de regime de juros é a mais utilizada no sistema financeiro. Nesse regime, os juros gerados em cada período são somados ao principal para calcular os juros do próximo período. Isso significa que os rendimentos gerados por uma aplicação são adicionados de volta à aplicação e participam da geração de rendimentos no próximo período.
Quando trabalhamos com juros compostos, o dinheiro cresce muito mais rapidamente. Neste caso, temos um crescimento exponencial em progressão geométrica ao longo do período. Esse modelo leva à expressão que ouvimos em nosso dia a dia: "juro sobre juro". O modelo descrito acima é conhecido também como regime de capitalização composta.
Vejamos o seguinte exemplo: Um capital (C) de R$ 1.000,00 aplicado a taxa (i) de 10% a.m. durante quatro meses (n). O montante ao término do período pode ser obtido diretamente na fórmula:
Logo, teríamos M = 1.000,00 (1+0,1)4 = R$ 1.464,10. Segundo Samanez (2002), os fatores (1 + i)^n e (1+ i)^-n têm a seguinte finalidade:
- O fator (1 + i)^n "joga" grandezas para frente, possibilitando encontrar o montante ou valor futuro da aplicação. É a capitalização para data posterior.
- O fator (1+ i)^-n "puxa" grandezas para trás, possibilitando encontrar o principal de um determinado montante, ou seja, traz um valor futuro à data anterior.
Conceito de Juros Compostos
O regime de juros compostos consiste em adicionar os juros formados em cada período ao capital original, resultando em um novo montante (capital + juros) que passa a ser o capital para o próximo período. Isso significa que os juros são capitalizados e, como resultado, não apenas o capital inicial gera rendimentos, mas também os juros gerados anteriormente. Portanto, denominamos esse regime de juros compostos.
A capitalização é o processo pelo qual os juros são adicionados ao principal, e é a principal diferença entre juros simples e compostos. Para ilustrar essa diferença, vamos considerar o exemplo a seguir.
Cálculo do juro
Como é do nosso conhecimento, o montante é a soma do principal aos juros da aplicação no prazo determinado e à taxa de juros estipulada. Para obtenção dos juros, temos a seguinte fórmula:
Exemplo: Determine o valor dos juros pagos em um empréstimo de R$ 2.000,00 com taxa de juros de 1% a.m. pelo período de cinco meses.
Resolução:
- VA = valor atual
- N = valor nominal
- i = taxa de juros
- n = número de períodos que antecede o vencimento do título.
O valor atual na data focal zero do título com vencimento em 12 meses é dado por:
O valor atual na data focal zero do título com vencimento em seis meses é dado por:
Taxas equivalentes
Consideram-se duas taxas como equivalentes, se na hipótese de aplicá-las a um mesmo prazo e a um
mesmo capital for indiferente aplicar em uma ou em outra.
- i = referente a um intervalo de tempo p;
- iq = corresponde a um intervalo de tempo igual a fração própria p/q onde q > p;
- i quero = é a taxa que pretendemos determinar
- i tenho = é a taxa que temos determinada.
EXERCÍCIO PROPOSTO
1. Uma calculadora é vendida por R$ 140,00 à vista ou em pagamento dividido em dois meses com uma taxa de juros compostos de 5% a.m. Qual o valor a ser pago?
2. Assumindo que você possui um título no valor de R$ 42.000,00 para pagamento daqui a três meses, que deverá ser substituído por outro título com vencimento daqui a cinco meses. Pergunta-se qual o valor a ser pago aceitando uma taxa de juros de 25% a.a. com juros compostos?
3. A rentabilidade efetiva de um investimento é de 10% a.a. Sabendo-se que os juros foram de R$ 27.473,00, o capital era de R$ 83.000,00. Qual o período de aplicação desse capital?
4. Por um equipamento de R$ 360.000,00 paga-se uma entrada de 20% mais dois pagamentos mensais e consecutivos. Considerando o primeiro pagamento de R$ 180.000,00 e a taxa de juros efetiva aplicada de 10% a.m., calcule o valor do segundo pagamento.
5. Um capital de R$ 50.000,00 rendeu R$ 1.000,00 em determinado prazo. Se o prazo fosse superior em dois meses, o rendimento aumentaria em R$ 2.060,40. Calcule a taxa de juros efetiva ao mês, ganha pela aplicação e o prazo em meses.
6. Dois capitais foram aplicados durante dois anos: o primeiro a juros efetivos de 2% a.m. e o segundo, a 1,5% a.m. O primeiro capital é R$ 10.000,00, superior ao segundo e seu rendimento excedeu em R$ 6.700,00 em relação ao rendimento do segundo capital. Calcule o valor de cada capital.
7. Suponha um capital aplicado a juros efetivos de 30% a.a. Depois de três anos, resgatou-se 50% dos juros ganhos, e depois o restante do montante foi aplicado com uma taxa efetiva de 32% a.a., obtendo-se rendimento de R$ 102,30 no prazo de um ano. Determine o valor aplicado inicialmente.
8. Um investidor aplicou R$ 1.000,00 em um fundo que paga 5% a.m., com o objetivo de dispor de R$ 1.102,50 após dois meses. Após 24 dias de aplicação, a taxa efetiva baixou para 4% a.m. Quanto tempo será necessário para obter o capital desejado?
9. Uma quantia de R$ 4.000,00 foi aplicada em dois investimentos diferentes, o primeiro com taxa de 6% a.t. e o segundo a uma taxa de 2% a.m. Sabendo que após oito meses o valor das parcelas se igualam, determine o valor de cada parcela.
10.Determinada quantia foi aplicada em um fundo e duplicou seu valor entre 11 de junho e 22 de novembro do mesmo ano. Determine a que taxa esse fundo foi aplicado.
11.(AFRF 2001) O desconto racional simples de uma nota promissória, 5 meses antes de seu vencimento é de R$ 800,00, a uma taxa de 4% a.m. Calcule o desconto comercial simples correspondente, isto é considerando o mesmo título, a mesma taxa e o mesmo prazo.
a) R$ 960,00
b) R$ 666,67
c)R$ 973,32
d) R$ 640,00
e) R$ 800,00